Question

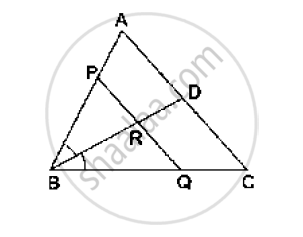
In ΔABC, the bisector of ∠B meets AC at D. A line OQ║AC meets AB, BC and BD at O, Q and R respectively. Show that BP × QR = BQ × PR 

 

Answer 1

In triangle BQO, BR bisects angle B.
Applying angle bisector theorem, we get: 

`(QR)/(PR)=(BQ)/(BP)` 

⟹BP × QR = BQ × PR
This completes the proof.