Advertisements
Advertisements
Question
ΔABC is right angled at A and AD⊥BC. If BC = 13cm and AC = 5cm, find the ratio of the areas of ΔABC and ΔADC.
Solution
In ΔABC and ΔADC, we have:
∠𝐵𝐴𝐶= ∠𝐴𝐷𝐶=90°
∠𝐴𝐶𝐵= ∠𝐴𝐶𝐷 (𝑐𝑜𝑚𝑚𝑜𝑛)
By AA similarity, we can conclude that Δ BAC~ Δ ADC.
Hence, the ratio of the areas of these triangles is equal to the ratio of squares of their corresponding sides.
∴ `(ar(ΔBAC))/(ar(ΔADC))=(BC)^2/(AC)^2`
⇒ `(ar (Δ BAC))/(9ar(Δ ADC))=13^2/5^2`
=` 169/25`
Hence, the ratio of areas of both the triangles is 169:25
APPEARS IN
RELATED QUESTIONS
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
The perimeter of two similar triangles are 30 cm and 24 cm. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
On a map, drawn to a scale of 1 : 250000, a triangular plot PQR of land has the following measurements :
PQ = 3cm, QR = 4 cm and angles PQR = 90°
(i) the actual lengths of QR and PR in kilometer.
(ii) the actual area of the plot in sq . km.
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

In the given figure, ∠CAB = 90° and AD⊥BC. Show that ΔBDA ~ ΔBAC. If AC = 75cm, AB = 1m and BC = 1.25m, find AD.

Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

State the SAS-similarity criterion
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
If ΔABC ~ ΔDEF, then writes the corresponding congruent angles and also write the ratio of corresponding sides.
Sides of a triangle are 7, 24 and 25. Determine whether the triangle is a right-angled triangle or not.
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
In the given figure, ABC is a triangle. DE is parallel to BC and `"AD"/"DB" = (3)/(2)`.
(i) Determine the ratios `"AD"/"AB","DE"/"BC"`.
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find `"EF"/"FB"`.
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that TP:TQ = TR:TS
In the given figure, PB is the bisector of ABC and ABC =ACB. Prove that:
a. BC x AP = PC x AB
b. AB:AC = BP: BC
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`

Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
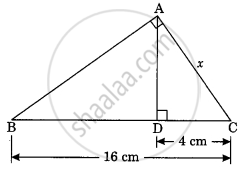
In the given figure the value of x is
∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
In ΔABC, PQ || BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

