Advertisements
Advertisements
प्रश्न
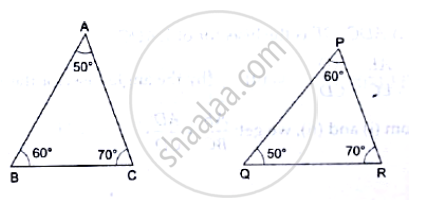
From the given figure, prove that ΔABC ~ ΔEDF
उत्तर
From the ΔABC, AB = AC
It is an isosceles triangle
Angles opposite to equal sides are equal
∴ ∠B = ∠C = 65°
∴ ∠B + ∠C = 65° + 65°
= 130°
We know that sum of three angles is a triangle = 180°
∠A + ∠B + ∠C = 180°
∠A + 130° = 180°
∠A = 180° – 130°
∠A = 50°
From ΔEDF, ∠E = 50°
∴ Sum of Remaining angles = 180° – 50° = 130°
DE = FD
∴ ∠D = ∠F
From ΔABC and ΔEDF
∴ ΔD = `130/2` = 65°
∠A = ∠E = 50°
∠B = ∠D = 65°
∠C = ∠F = 65°
∴ By AAA criteria ΔEDF ~ ΔABC
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
In the figure, AB || RQ and BC || SQ, prove that `"PC"/"PS" = "PA"/"PR"`.
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
In ∠BAC = 90° and AD ⊥ BC. A then ______.

In ΔABC, PQ || BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

