Advertisements
Advertisements
Question
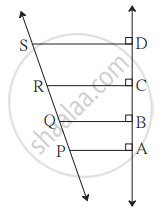
In the given figure, seg PA, seg QB, seg RC, and seg SD are perpendicular to line AD.
AB = 60, BC = 70, CD = 80, PS = 280 then find PQ, QR, and RS.
Notes

`{:("seg PA, seg QB, seg RC, and seg SD are perpendicular to line AD."),("AB = 60, BC = 70, CD = 80, PS = 280"):} ...}"Given"`
AD = AB + BC + CD
∴ AD = 60 + 70 + 80
∴ AD = 210
The lines PA, QB, RC, and SD are parallel to each other.
The Intercept theorem provides the ratios between the line segments created when two parallel lines are intercepted by two intersecting lines.
By the Intercept Theorem,
`"PQ"/"AB" = "QR"/"BC" = "RS"/"CD" = "PS"/"AD"`
∴ `"PQ"/60 = "QR"/70 = "RS"/80 = 280/210`
Considering `"PQ"/60 = 280/210`,
∴ `"PQ"/60 = 280/210`
∴ `"PQ" = (280 × 60)/210`
∴ PQ = 80
Considering `"QR"/70 = 280/210`
∴ `"QR"/70 = 280/210`
∴ `"QR" = (280 × 70)/210`
∴ `"QR" = 280/3`
Considering `"RS"/80 = 280/210`
∴ `"RS"/80 = 280/210`
∴ `"RS" = (280 × 80)/210`
∴ `"RS" =320/3`
RELATED QUESTIONS
In ∆PQR, PM = 15, PQ = 25 PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.

In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, Find BQ.

In the given fig, XY || seg AC. If 2AX = 3BX and XY = 9. Complete the activity to Find the value of AC.
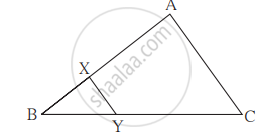
Activity: 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX" +"BX")/"BX" = (square + square)/square` ...(by componendo)
`"AB"/"BX" = square/square` ...(I)
ΔBCA ~ ΔBYX ...`square` test of similarity,
∴ `"BA"/"BX" = "AC"/"XY"` ...(corresponding sides of similar triangles)
∴ `square/square = "AC"/9`
∴ AC = `square` ...[From(I)]
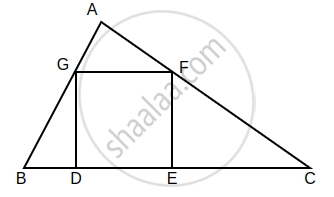
In the given figure, the vertices of square DEFG are on the sides of ∆ABC. ∠A = 90°. Then prove that DE2 = BD × EC. (Hint: Show that ∆GBD is similar to ∆CFE. Use GD = FE = DE.)

In the above figure, line l || line m and line n is a transversal. Using the given information find the value of x.

In the above figure, line AB || line CD || line EF, line l, and line m are its transversals. If AC = 6, CE = 9. BD = 8, then complete the following activity to find DF.
Activity :
`"AC"/"" = ""/"DF"` (Property of three parallel lines and their transversal)
∴ `6/9 = ""/"DF"`
∴ `"DF" = "___"`
