Advertisements
Advertisements
प्रश्न
A magnetic field set up using Helmholtz coils is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 × 10–5 V m–1, make a simple guess as to what the beam contains. Why is the answer not unique?
उत्तर
Magnetic field, B = 0.75 T
Accelerating voltage, V = 15 kV = 15 × 103 V
Electrostatic field, E = 9 × 10–5 V m−1
Mass of the electron = m
Charge of the electron = e
Velocity of the electron = v
Kinetic energy of the electron = eV
`1/2"mv"^2` = eV
∴ `"e"/"m" = "v"^2/(2"V")` ..........(1)
Since the particle remains undeflected by electric and magnetic fields, we can infer that the force on the charged particle due to electric field is balancing the force on the charged particle due to magnetic field.
∴ eE = evB
v = `"E"/"B"` ............(2)
Putting equation (2) in equation (1), we get
`"e"/"m" = 1/2(("E"/"B")^2)/"V" = "E"^2/(2"VB"^2)`
= `(9.0 xx 10^-5)^2/(2 xx 15000 xx (0.75)^2)`
= 4.8 × 107 C/kg
This value of specific charge e/m is equal to the value of deuteron or deuterium ions. This is not a unique answer. Other possible answers are He++, Li++, etc.
APPEARS IN
संबंधित प्रश्न
Use this law to find magnetic field due to straight infinite current carrying wire.
Magnetic lines of force always cross each other
A charge ‘q’ moving along the X- axis with a velocity `vecv` is subjected to a uniform magnetic field B along the Z-axis as it crosses the origin O.
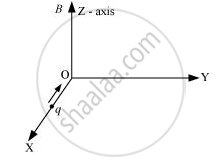
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
Two wires carrying equal currents i each, are placed perpendicular to each other, just avoiding a contact. If one wire is held fixed and the other is free to move under magnetic forces, what kind of motion will result?
According to the right-hand rule, the direction of magnetic induction if the current is directed in an anticlockwise direction is ______
Assertion: Free electrons always keep on moving in a conductor even then no magnetic force act on them in magnetic field unless a current is passed through it.
Reason: The average velocity of free electron is zero.
The correct plot of the magnitude of magnetic field `vec"B"` vs distance r from centre of the wire is, if the radius of wire is R.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
In the product
`overset(->)("F") = "q"(overset(->)(υ) xx overset(->)("B"))`
= `"q"overset(->)(υ) xx ("B"overset(^)("i") + "B" overset(^)("j") + "B"_0overset(^)("k"))`
For q = 1 and `overset(->)(υ) = 2overset(^)("i") + 4overset(^)("j") + 6overset(^)("k")` and
`overset(->)("F") = 4overset(^)("i") - 20overset(^)("j") + 12overset(^)("k")`
What will be the complete expression for `overset(->)("B")`?
