Advertisements
Advertisements
प्रश्न
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h –1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h–1.
- What is the magnitude of average velocity, and
- average speed of the man over the interval of time
- 0 to 30 min,
- 0 to 50 min,
- 0 to 40 min?
[Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero!]
उत्तर
Time taken by the man to reach the market from home, `t_1 = 2.5/5 = 0.5 = 30 min`
Time taken by the man to reach home from the market, `t_2 = 2.5/7.5 = 0.333 = 20 min`
Total time taken in the whole journey = 30 + 20 = 50 min
(i) Over the interval of time 0 to 30 min:
`"Average velocity" = "Displacement"/"Time" = 2.5/0.5 = 5 "km/h"`
`"Average speed" = "Distance"/"Time" = 2.5/0.5 = 5 "km/h"`
(ii) Over the interval of time 0 to 50 min:
Time = 50 min = `5/6 h`
Net displacement = 0
Total distance = 2.5 + 2.5 = 5 km
`"Average velocity" = "Displacement"/"Time" = 0/(5/6) = 0`
`"Average speed" = "Distance"/"Time" = 5/(5/6) = 6 "km/h"`
(iii) Over the interval of time 0 to 40 min:
Speed of the man = 7.5 km
Distance travelled in first 30 min = 2.5 km
Distance travelled by the man (from market to home) in the next 10 min `= 7.5xx 10/60 = 1.25`
Net displacement = 2.5 - 1.25 = 1.25 km
Total distance travelled = 2.5 + 1.25 = 3.75 km
`"Average velocity" = 1.25/(40/60) = (1.25xx3)/2 = 1.875 "km/h"`
Average speed =`3.75/(40/60) = 5.625 "km/h"`
APPEARS IN
संबंधित प्रश्न
A woman starts from her home at 9.00 am, walks with a speed of 5 km h–1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h–1. Choose suitable scales and plot the x-t graph of her motion.
In Exercise, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
Suggest a suitable physical situation for the following graph:
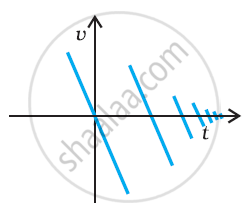
Write the SI units of speed and average speed.
Two cars are moving with speeds of 40 km/hr due North and 40 km/hr due South respectively. Do they have the same velocity?
In one dimensional motion, instantaneous speed v satisfies 0 ≤ v < v0.
The displacement of a particle is given by x = (t – 2)2 where x is in metres and t in seconds. The distance covered by the particle in first 4 seconds is ______.
A particle executes the motion described by x(t) = x0 (1 − e − γt); t ≥ 0, x0 > 0. Where does the particle start and with what velocity?
A particle executes the motion described by x(t) = x0(1 − e −γt); t ≥ 0, x0 > 0. Find maximum and minimum values of x(t), v(t), a(t). Show that x(t) and a(t) increase with time and v(t) decreases with time.
A monkey climbs up a slippery pole for 3 seconds and subsequently slips for 3 seconds. Its velocity at time t is given by v(t) = 2t (3 – t); 0 < t < 3 and v(t) = – (t – 3)(6 – t) for 3 < t < 6 s in m/s. It repeats this cycle till it reaches the height of 20 m.
- At what time is its velocity maximum?
- At what time is its average velocity maximum?
- At what time is its acceleration maximum in magnitude?
- How many cycles (counting fractions) are required to reach the top?
