Advertisements
Advertisements
प्रश्न
A mason uses the expression x2 + 6x + 8 to represent the area of the floor of a room. If the decides that the length of the room will be represented by (x + 4), what will the width of the room be in terms of x?
उत्तर
Given length of the room = x + 4
Area of the room = x2 + 6x + 8
Length × breadth = x2 + 6x + 8
breadth = `(x^2 + 6x + 8)/(x + 4)` ...(1)
Factorizing x2 + 6x + 8, it is in the form of ax2 + bx + c
Where a = 1, b = 6, c = 8
The product a × c = 1 × 8 = 8
sum = b = 6
| Product = 8 | Sum = 6 |
| 1 × 8 = 8 | 1 + 8 = 9 |
| 2 × 4 = 8 | 2 + 4 = 6 |
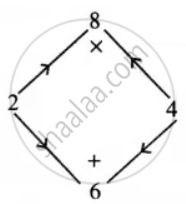
The middle term 6x can be written as 2x + 4x
∴ x2 + 6x + 8 = x2 + 2x + 4x + 8
= x(x + 2) + 4(x + 2)
x2 + 6x + 8 = (x + 2)(x + 4)
Now from (1)
breadth = `(x^2 + 6x + 8)/(x + 4)`
= `((x + 2)(x + 4))/((x + 4))`
= x + 2
∴ Width of the room = x + 2
APPEARS IN
संबंधित प्रश्न
Factorize each of the following expression:
a4 − 16b4
Factorize each of the following expression:
x8 − 1
Factorize each of the following expression:
x4 − 1
Factorize each of the following expression:
x − y − x2 + y2
Factorize each of the following expression:
16(2x − 1)2 − 25y2
Factorize each of the following expression:
4(xy + 1)2 − 9(x − 1)2
Factorize each of the following expression:
2a5 − 32a
Factorize each of the following quadratic polynomials by using the method of completing the square:
4y2 + 12y + 5
Factorize each of the following quadratic polynomials by using the method of completing the square:
x2 + 12x + 20
Factorize each of the following quadratic polynomials by using the method of completing the square:
a2 − 14a − 51
