Advertisements
Advertisements
प्रश्न
A point P(a, b) is reflected in the X-axis to P'(2, – 3). Write down the value of a & b. P” is the image of P, when reflected on the Y-axis. Write down the co-ordinates of P” when P is reflected in the line parallel to the Y-axis, such that x = 4.
उत्तर
Reflection of P (a, b) on the X-axis P' (a, -b)
(i) ∴ P' (a, -b) = P' (2, -3)
+ a = + 2, ∴ a = 2
-b = -3, ∴ b = 3
P (2, 3)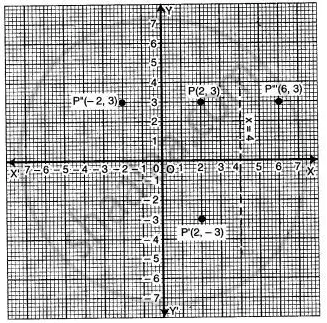
(ii) P'' is the image of P(2, 3) under reflection Y-axis = P''(-2, 3).
(iii) P''' is the image of P(2, 3) under reflection x = 4
⇒ P'''(6, 3).
APPEARS IN
संबंधित प्रश्न
Complete the following table:
| Point | Transformation | Image | |
| (a) | (5, –7) | -------------------- | (–5, 7) |
| (b) | (4, 2) | Reflection in x-axis | ------- |
| (c) | ------- | Reflection in y-axis | (0, 6) |
| (d) | (6, –6) | -------------------- | (–6, 6) |
| (e) | (4, –8) | -------------------- | (–4, –8) |
State the co-ordinates of the following point under reflection in the line x = 0:
(–6, 4)
A point P is reflected in the x-axis. Co-ordinates of its image are (–4, 5). Find the co-ordinates of P.
A point P is reflected in the x-axis. Co-ordinates of its image are (–4, 5). Find the co-ordinates of the image of P under reflection in the y-axis.
The point P(a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (4, 6); evaluate a and b.
A point P is mapped onto P' under the reflection in the x-axis. P' is mapped onto P" under the reflection in the origin. If the co-ordinates of
P" are (5,-2), write down the co-ordinates of P. State the single transformation that takes place.
Write down the co-ordinates of the image of (5, – 4).
Reflection in y = 2.
Using a graph paper, plot the points A (6,4) and B (0,4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for. the figure ABA’B’.
(iv) Find its perimeter.
(i) Point P(a, b) reflected on the X-axis to P'(5, 2). Write down the value of a and b.
(ii) P” is the image of P when reflected on the Y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”.
Use a graph paper to answer the following questions. (Take 1 cm = 1 unit on both axis):
(i) Plot A (4, 4), B (4, – 6) and C (8, 0), the vertices of a triangle ABC.
(ii) Reflect ABC on the y-axis and name it as A’B’C’.
(iii) Write the coordinates of the images A’, B’ and C’.
(iv) Give a geometrical name for the figure AA’ C’B’ BC.
(v) Identify the line of symmetry of AA’ C’ B’ BC.
