Advertisements
Advertisements
प्रश्न
Use a graph paper to answer the following questions. (Take 1 cm = 1 unit on both axis):
(i) Plot A (4, 4), B (4, – 6) and C (8, 0), the vertices of a triangle ABC.
(ii) Reflect ABC on the y-axis and name it as A’B’C’.
(iii) Write the coordinates of the images A’, B’ and C’.
(iv) Give a geometrical name for the figure AA’ C’B’ BC.
(v) Identify the line of symmetry of AA’ C’ B’ BC.
उत्तर
(i) and (ii) see the given graph.
(iii) A' (-4, 4), B' (-4, -6), C' (-8, 0).
(iv) AA' C'' B' BC is a Hexagon.
(v) y-axis is the line of symmetry.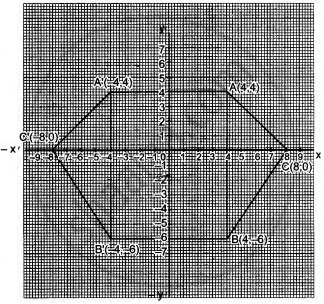
APPEARS IN
संबंधित प्रश्न
State the co-ordinates of the following point under reflection in y-axis:
(6, –3)
A point P is reflected in the x-axis. Co-ordinates of its image are (–4, 5). Find the co-ordinates of P.
The point P(a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (4, 6); evaluate a and b.
State the co-ordinates of the following point under reflection in x-axis:
(–5, 4)
The image of a point P under reflection on the X-axis is (5, – 2). Write down the co-ordinates of P.
Write down the co-ordinates of the image of (5, – 4).
Reflection in y = 2.
Using a graph paper, plot the points A (6,4) and B (0,4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for. the figure ABA’B’.
(iv) Find its perimeter.
A point P(4, – 1) is reflected to P’ in the line y = 2 followed by the reflection to P” in the line x = -1. Find :
(i) The co-ordinates of P’.
(ii) The co-ordinates of P”.
(iii) The length of PP’.
(iv) The length of P’P”.
(i) Point P(a, b) reflected on the X-axis to P'(5, 2). Write down the value of a and b.
(ii) P” is the image of P when reflected on the Y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”.
Use graph paper for this question.
The point P (5, 3) was reflected in the origin to get the image P’.
(i) Write down the co-ordinates of P’.
(ii) If M is the foot of the perpendicular from of P to the X-axis, find the co-ordinates of M.
(iii) If N is the foot of the perpendicular from of P’ to the X-axis, find the co-ordinates of N.
(iv) Name the figure PMP’N.
(v) Find the area of die figure PMP’N.
