Advertisements
Advertisements
प्रश्न
Use a graph paper to answer the following questions. (Take 1 cm = 1 unit on both axis):
(i) Plot A (4, 4), B (4, – 6) and C (8, 0), the vertices of a triangle ABC.
(ii) Reflect ABC on the y-axis and name it as A’B’C’.
(iii) Write the coordinates of the images A’, B’ and C’.
(iv) Give a geometrical name for the figure AA’ C’B’ BC.
(v) Identify the line of symmetry of AA’ C’ B’ BC.
उत्तर
(i) and (ii) see the given graph.
(iii) A' (-4, 4), B' (-4, -6), C' (-8, 0).
(iv) AA' C'' B' BC is a Hexagon.
(v) y-axis is the line of symmetry.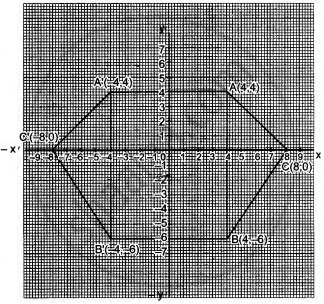
APPEARS IN
संबंधित प्रश्न
State the co-ordinates of the following point under reflection in y-axis:
(6, –3)
A point P is reflected in the origin. Co-ordinates of its image are (–2, 7). Find the co-ordinates of the image of P under reflection in the x-axis.
The point P(a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (4, 6); evaluate a and b.
The point P(x, y) is first reflected in the x-axis and reflected in the origin to P’. If P’ has co-ordinates (–8, 5); evaluate x and y.
A triangle ABC lies in the co-ordinate plane. The co-ordinates of its vertices are A (2, 3), B ( 4,-4) and C (6 ,-7). This triangle is reflected in the line y=O onto LA'B'C'. LA'B'C' is then reflected in the origin ontolA"B"C". Write down the co-ordinates of LA'B'C' and LA "B" C".
State the co-ordinates of the following point under reflection in x-axis:
(–5, 4)
Write down the co-ordinates of the image of (5, – 4).
Reflection in y = 2.
P, Q have co-ordinates (-1, 2) and (6, 3) respectively. Reflect P on the X-axis to P’. Find:
(i) The co-ordinate of P’
(ii) Length of P’Q.
(iii) Length of PQ.
(iv) Is P’Q = PQ?
(i) Point P(a, b) reflected on the X-axis to P'(5, 2). Write down the value of a and b.
(ii) P” is the image of P when reflected on the Y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”.
The point P(3, 4) is reflected to P’ in the x-axis and O’ is the image of O (the Origin) in the line PP’ Find :
(i) The coordinates of P’ and O’.
(ii) The length of segment PP’ and OO’.
(iii) The perimeter of the quadrilateral POP’O’
(iv) What is the special name of the quadrilateral POP’O’.
