Advertisements
Advertisements
प्रश्न
A quadrilateral ABCD has exactly one axis of symmetry, which is not a diagonal. Show that the quadrilateral is an isosoeles trapezium.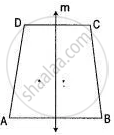
उत्तर
Consider a quadrilateral ABCD.
Let m be a line which is not a diagonal of quad. ABCD.
Let the quad. ABCD have this line only as its axis of symmetry.
Then A, B and D, C are the two pairs of points each pair symmetric w.r.t., line m.
∴ Line m is the perpendicular bisector of AB as well as DC.
⇒ AB || DC ...(1)
Also AD and BC are symmetric w.r.t., line m.
∴ AD = BC ...(2)
In view of (1) and (2), quadrilateral ABCD is an isosceles trapezium.
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the figure given below, draw the line (s) of symmetry, if possible:

In the figure given below, draw the line (s) of symmetry, if possible:
Draw a quadrilateral with exactly three lines of symmetry. In case, if possible, represent the line/ lines of symmetry by dotted lines. Also, write the special name of the quadrilateral drawn.
Draw a quadrilateral with more than four lines of symmetry. In case, if possible, represent the line/ lines of symmetry by dotted lines. Also, write the special name of the quadrilateral drawn.
In each of the figure below, state the number of axes of symmetry, if any.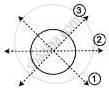
Give half a turn to the numbers from 0 to 9. Find which of them still looks the same.
Which of the following has a line of symmetry?
Draw all lines of symmetry for the following figure as given below:

Draw all lines of symmetry for the following figure as given below:

The flag of Japan is shown below. How many lines of symmetry does the flag have?

