Advertisements
Advertisements
प्रश्न
A quadrilateral ABCD has exactly one axis of symmetry, which is not a diagonal. Show that the quadrilateral is an isosoeles trapezium.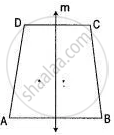
उत्तर
Consider a quadrilateral ABCD.
Let m be a line which is not a diagonal of quad. ABCD.
Let the quad. ABCD have this line only as its axis of symmetry.
Then A, B and D, C are the two pairs of points each pair symmetric w.r.t., line m.
∴ Line m is the perpendicular bisector of AB as well as DC.
⇒ AB || DC ...(1)
Also AD and BC are symmetric w.r.t., line m.
∴ AD = BC ...(2)
In view of (1) and (2), quadrilateral ABCD is an isosceles trapezium.
Hence proved.
APPEARS IN
संबंधित प्रश्न
A( 4, 1 ), B(2,3) and C( 5,6) are the vertices of a figure which is symmetrical about x=7. Complete the figure and give the geometrical name of the figure if any.
In the figure given below, draw the line (s) of symmetry, if possible:
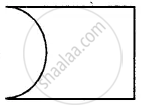
In the figure given below, draw the line (s) of symmetry, if possible:

In the figure given below, draw the line (s) of symmetry, if possible:
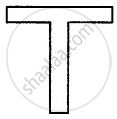
Draw a triangle with exactly two lines of symmetry. In case, if possible, represent the line/ lines of symmetry by dotted lines. Also, write the special name of the triangle drawn.
In the figure given below, draw the line (s) of symmetry, if possible:
Write the capital letters of the English alphabet in your notebook. Try to draw their axes of symmetry. Which ones have an axis of symmetry? Which ones have more than one axis of symmetry?
Draw the axes of symmetry of the figure below. Which of them has more than one axis of symmetry?
Draw the mirror image:
One day his clever daughter gave him an idea which he liked very much. Now he never got confused.
- Can you guess what the idea was?