Advertisements
Advertisements
प्रश्न
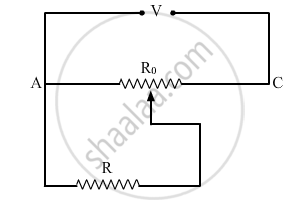
A resistance of R Ω draws current from a potentiometer as shown in the figure. The potentiometer has a total resistance Ro Ω. A voltage V is supplied to the potentiometer. Derive an expression for the voltage across R when the sliding contact is in the middle of the potentiometer.
उत्तर
From the figure given in the question, current I through Ro is
`I=V/R_o`
Now, the sliding contact is in the middle of the wire. From the relation `R=rhol/A`
R ∝ l (where ρ and A are constants)
where l is the length of the wire, ρ is the resistivity and A is the area of the wire.
∴ Resistance of half of the wire of the potentiometer is
`R'=R_o/2`
Now R' and R are in parallel; therefore, voltage across R and R' is equal. Therefore, voltage across R is
`:.V'=I.R'=V/R_o"."R_o/2`
`=>V'=V/2`
APPEARS IN
संबंधित प्रश्न
The instrument which can measure terminal potential difference as well as electromotive force (e.m. f.) is ______
- Wheatstone’s meter bridge
- Voltmeter
- Potentiometer
- Galvanometer
A cell balances against a length of 200 cm on a potentiometer wire, when it is shunted by a resistance of 8Ω. The balancing length reduces by 40 cm, when it is shunted by a resistance of 4 Ω . Calculate the balancing length when the cell is in open circuit. Also calculate the internal resistance of the cell.
Which material is used for the meter bridge wire and why?
In a metre bridge, the balance point is found at a distance l1 with resistances R and S as shown in the figure.An unknown resistance X is now connected in parallel to the resistance S and the balance point is found at a distance l2. Obtain a formula for X in terms of l1, l2 and S.

In a meter bridge, the null point is found at a distance of l1 cm from A. If now a resistance of X is connected in parallel with S, the null point occurs at l2 cm. Obtain a formula for X in terms of l1, l2 and S.

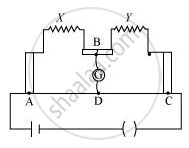
The figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10 Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10 Ω resistance is instead connected in series with resistance ‘Y’. Determine the values of the resistances X and Y.
Two resistances are connected in the two gaps of a meter bridge. The balance points is 20 cm from the zero end. When resistance of 15 ohm is connected in series with the smaller of the two resistances, the null point shifts to 40 cm. The smaller of the two resistances has the value (in ohm) ______.
The metre bridge works on the principle of ______
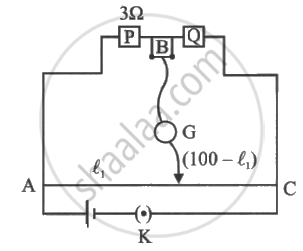
In a meter bridge experiment, resistance are connected as shown in figure, The balancing length 1, is 55 cm. Now an unknown resistance x is connected in series with P and new balancing length is found to be 75cm. The value of x is ______.
A meter bridge is balanced with a known resistance (R) in the left hand gap and an unknown resistance (S) in the right hand gap. Balance point is found to be at a distance of 1 cm from the left hand side. When the battery and the galvanometer are interchanged, balance point will ______.
