Question

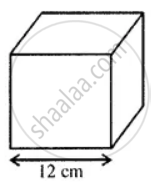
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.

Answer 1

Here, the cube of side 12 cm is divided into 8 cubes of side 9 cm.

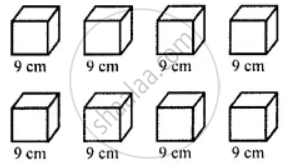
Given that,

Their volumes are equal.

The volume of big cube of 12 cm = Volume of 8 cubes of side a cm

(Side of the big cube)³ = 8 x (Side of the small cube)³
(12)³ = 8 x a³

⇒ `a^3 = (12 xx 12 xx 12)/8`

⇒ `a^3 = 6^3` cm³

⇒ a = 6 cm

Ratio of their surface = `"Surface area of the original cube"/"Total surface area of the small cube"`

= `(6("side of big cube")^2)/(8 xx 6("side of small cube")^2)`

= `(6 xx 12 xx 12)/(8 xx 6 xx 6 xx 6) = 4/8 = 1:2`

So, the ratio is 1:2