Advertisements
Advertisements
Question
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
Solution
Here, the cube of side 12 cm is divided into 8 cubes of side 9 cm.
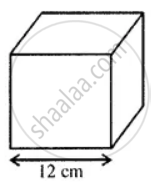
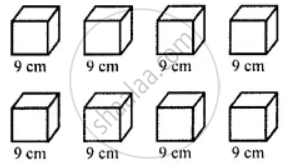
Given that,
Their volumes are equal.
The volume of big cube of 12 cm = Volume of 8 cubes of side a cm
(Side of the big cube)3 = 8 x (Side of the small cube)3
(12)3 = 8 x a3
⇒ `a^3 = (12 xx 12 xx 12)/8`
⇒ `a^3 = 6^3` cm3
⇒ a = 6 cm
Ratio of their surface = `"Surface area of the original cube"/"Total surface area of the small cube"`
= `(6("side of big cube")^2)/(8 xx 6("side of small cube")^2)`
= `(6 xx 12 xx 12)/(8 xx 6 xx 6 xx 6) = 4/8 = 1:2`
So, the ratio is 1:2
APPEARS IN
RELATED QUESTIONS
The dimensions of a metal block are 2.25 m by 1.5 m by 27 cm. It is melted and recast into cubes, each of the side 45 cm. How many cubes are formed?
Find the surface area of a cube whose volume is 216 dm3.
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
The internal length, breadth, and height of a box are 30 cm, 24 cm, and 15 cm. Find the largest number of cubes which can be placed inside this box if the edge of each cube is
(i) 3 cm (ii) 4 cm (iii) 5 cm
The dimensions of a solid metallic cuboid are 72 cm × 30 cm × 75 cm. It is melted and recast into identical solid metal cubes with each edge 6 cm. Find the number of cubes formed.
Also, find the cost of polishing the surfaces of all the cubes formed at the rate Rs. 150 per sq. m.
Three equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the resulting cuboid to that of the sum of the total surface areas of the three cubes.
The base of a rectangular container is a square of side 12 cm. This container holds water up to 2 cm from the top. When a cube is placed in the water and is completely submerged, the water rises to the top and 224 cm3 of water overflows. Find the volume and surface area of the cube.
The lateral surface area of a cube of side 12 cm is
If the lateral surface area of a cube is 600 cm2, then the total surface area is
The total surface area of a cube is 96 cm2. The volume of the cube is ______.
