Advertisements
Advertisements
Question
The diameter of a garden roller is 1.4 m and it 2 m long. Find the maximum area covered by its 50 revolutions?
Solution
Diameter of the roller = 1.4 m
Radius (r) = `1.4/2` = 0.7 m
and length (h) = 2m
Curved surface area = 2πrh = 2 x `22/7` x 0.7 x 2 cm2 = 8.8 m2
Area covered in 50 complete revolutions = 8.8 x 50 m2 = 440 m2
Area of the playground = 440 m2
APPEARS IN
RELATED QUESTIONS
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high. How much of tape is needed for all the 12 edges?
Find the lateral surface area and total surface area of a cuboid of length 80 cm, breadth 40 cm and height 20 cm.
The cost of preparing the walls of a room 12 m long at the rate of Rs. 1.35 per square metre is Rs. 340.20 and the cost of matting the floor at 85 paise per square metre is Rs. 91.80. Find the height of the room.
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions islength = 4 m, breadth = 2.5 m, height = 50 cm.
A tank is 8 m long, 6 m broad and 2 m high. How much water can it contain?
A rectangular field is 70 m long and 60 m broad. A well of dimensions 14 m × 8 m × 6 m is dug outside the field and the earth dug-out from this well is spread evenly on the field. How much will the earth level rise?
A swimming pool is 20 m long 15 m wide and 3 m deep. Find the cost of repairing the floor and wall at the rate of Rs 25 per square metre.
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the wall.
The external dimensions of a closed wooden box are 48 cm, 36 cm, 30 cm. The box is made of 1.5 cm thick wood. How many bricks of size 6 cm × 3 cm × 0.75 cm can be put in this box?
The surface area of a cuboid is 1300 cm2. If its breadth is 10 cm and height is 20 cm2, find its length.
If the areas of the adjacent faces of a rectangular block are in the ratio 2 : 3 : 4 and its volume is 9000 cm3, then the length of the shortest edge is
The cost of constructing a wall 8 m long, 4 m high and 10 cm thick at the rate of Rs. 25 per m3 is
10 cubic metres clay is uniformly spread on a land of area 10 ares. the rise in the level of the ground is
If the sum of all the edges of a cube is 36 cm, then the volume (in cm3) of that cube is
If l is the length of a diagonal of a cube of volume V, then
If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then `A/V`
A closed rectangular box is made of wood of 1.5 cm thickness. The exterior length and breadth are respectively 78 cm and 19 cm, and the capacity of the box is 15 cubic decimeters. Calculate the exterior height of the box.
Four cubes, each of edge 9 cm, are joined as shown below :

Write the dimensions of the resulting cuboid obtained. Also, find the total surface area and the volume
The curved surface area of a cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
The total surface area of a cylinder is 6512 cm2 and the circumference of its bases is 88 cm. Find:
(i) its radius
(ii) its volume
In a building, there are 24 cylindrical pillars. For each pillar, the radius is 28 m, and the height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m2.
A metallic sheet is of the rectangular shape with dimensions 48cm x 36cm. From each one of its corners, a square of 8cm is cutoff. An open box is made of the remaining sheet. Find the volume of the box.
Three identical cubes of side 4 cm are joined end to end. Find the total surface area and lateral surface area of the new resulting cuboid
The total surface area of a cuboid with dimension 10 cm × 6 cm × 5 cm is
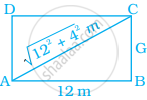
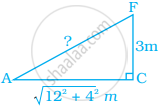
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.
External dimensions of a closed wooden box are in the ratio 5:4:3. If the cost of painting its outer surface at the rate of Rs 5 per dm2 is Rs 11,750, find the dimensions of the box.
