Advertisements
Advertisements
प्रश्न
A student has focused the image of a candle flame on a white screen using a concave mirror. The situation is as given below:
Length of the flame = 1.5 cm
Distance of flame from the mirror = 18 cm
If the flame is perpendicular to the principal axis of the mirror, then calculate the following:
- Distance of the image from the mirror
- Length of the image
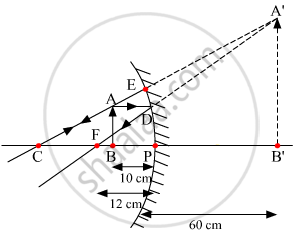
If the distance between the mirror and the flame is reduced to 10 cm, then what would be observed on the screen? Draw ray diagram to justify your answer for this situation.
उत्तर
Given:
Length of the flame, hO = 1.5 cm
Focal length of the mirror, f = −12 cm
Distance of flame from the mirror, u = −18 cm
(a) Let the distance of the image from the mirror be v.
According to mirror formula,
\[\frac{1}{f} = \frac{1}{v} + \frac{1}{u}\]
\[ \Rightarrow \frac{1}{\left( - 12 \right)} = \frac{1}{\left( - 18 \right)} + \frac{1}{v}\]
\[ \Rightarrow \frac{1}{v} = \frac{1}{\left( - 12 \right)} + \frac{1}{18}\]
\[ \Rightarrow \frac{1}{v} = \frac{- 3 + 2}{36} = \frac{- 1}{36}\]
\[ \Rightarrow v = - 36 cm\]
The image will be formed at a distance of 36 cm from the mirror on the same side of the mirror as that of the object.
(b) Using the formula of magnification, we have
\[m = - \frac{v}{u} = \frac{h_I}{h_O}\]
Where,
hI = Length of image
hO = Length of object (Candle flame)
On substituting the respective values, we get
\[m = - \frac{\left( - 36 \right)}{\left( - 18 \right)} = \frac{h_I}{1 . 5}\]
\[ \Rightarrow - 2 = \frac{h_I}{1 . 5}\]
\[ \Rightarrow h_I = - 3 cm\]
Hence, the length of image is 3 cm.
If the distance between the mirror and the flame is reduced to 10 cm, then the position of the image can be found using mirror formula given below:
Ray diagram of an object placed at a distance of 10 cm from the mirror.
APPEARS IN
संबंधित प्रश्न
An object is placed at the following distances from a concave mirror of focal length 15 cm, turn by turn:
(a) 35 cm
(b) 30 cm
(c) 20 cm
(d) 10 cm
Which position of the object will produce:
(i) a magnified real image?
(ii) a magnified virtual image?
(iii) a diminished real image?
(iv) an image of same size as the object?
An object is placed just outside the principal focus of concave mirror. Draw a ray diagram to show how the image is formed, and describe its size, position and nature.
Draw and complete the following diagrams to show what happens to the beams of light as they enter the glass block and then leave it:
In which equipment/s do you find ___________________
Choose the correct option from given alternative:
Consider the following properties of virtual images:
(A) cannot be projected on the screen
(B) are formed by both concave and convex lens
(C) are always erect
(D) are always inverted
Concave mirrors are used by dentists to examine teeth. Why?
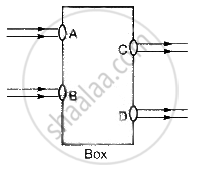
Beams of light are incident through the holes A and B and emerge out of box through the holes C and D respectively as shown in the figure. Which of the following could be inside the box?
The mirror having reflection surface curved outward ______.
A concave mirror produces a magnification of +4. The object is placed ______.
To obtain an image twice the size of the object, between which two points related to a concave mirror should an object be placed?
