Question

A student has focused the image of a candle flame on a white screen using a concave mirror. The situation is as given below:

Length of the flame = 1.5 cm

Focal length of the mirror = 12 cm

Distance of flame from the mirror = 18 cm

If the flame is perpendicular to the principal axis of the mirror, then calculate the following:

1. Distance of the image from the mirror
2. Length of the image

If the distance between the mirror and the flame is reduced to 10 cm, then what would be observed on the screen? Draw ray diagram to justify your answer for this situation.

Answer 1

Given:

Length of the flame, hO = 1.5 cm

Focal length of the mirror, f = −12 cm

Distance of flame from the mirror, u = −18 cm

(a) Let the distance of the image from the mirror be v.

According to mirror formula,

\[\frac{1}{f} = \frac{1}{v} + \frac{1}{u}\]

\[ \Rightarrow \frac{1}{\left( - 12 \right)} = \frac{1}{\left( - 18 \right)} + \frac{1}{v}\]

\[ \Rightarrow \frac{1}{v} = \frac{1}{\left( - 12 \right)} + \frac{1}{18}\]

\[ \Rightarrow \frac{1}{v} = \frac{- 3 + 2}{36} = \frac{- 1}{36}\]

\[ \Rightarrow v = - 36 cm\]

The image will be formed at a distance of 36 cm from the mirror on the same side of the mirror as that of the object.

(b) Using the formula of magnification, we have

\[m = - \frac{v}{u} = \frac{h_I}{h_O}\]

Where,

hI = Length of image

hO = Length of object (Candle flame)

On substituting the respective values, we get

\[m = - \frac{\left( - 36 \right)}{\left( - 18 \right)} = \frac{h_I}{1 . 5}\]

\[ \Rightarrow - 2 = \frac{h_I}{1 . 5}\]

\[ \Rightarrow h_I = - 3 cm\]

Hence, the length of image is 3 cm.

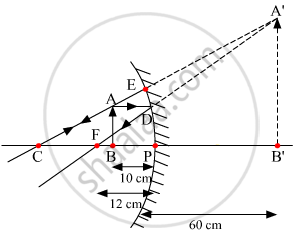
If the distance between the mirror and the flame is reduced to 10 cm, then the position of the image can be found using mirror formula given below:

\[\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\]

\[\frac{1}{v} = \frac{1}{f} - \frac{1}{u}\]

\[\frac{1}{v} = \frac{1}{\left( - 12 \right)} - \frac{1}{\left( - 10 \right)}\]

\[v = 60 cm\]

In this case, a virtual and erect image will be formed behind the mirror. Therefore, nothing will be observed on the screen.
Ray diagram of an object placed at a distance of 10 cm from the mirror.​