Advertisements
Advertisements
प्रश्न
A student said that the ratios `3/4` and `9/16` were proportional. What error did the student make?
उत्तर
Two ratios a : b and c : d are said to be proportional
if `a/b = c/d` or ad = bc.
But the given ratios `3/4` and `9/16, 3 × 6 ≠ 4 × 9`
Hence, the ratios are not proportional. To make a ratio proportional to another ratio, we just simply multiply both numerator and denominator by the same number. Here, the student had multiply numerator by 3 and denominator by 4, which is incorrect.
APPEARS IN
संबंधित प्रश्न
If a, b, c and d are in proportion prove that `sqrt((4a^2 + 9b^2)/(4c^2 + 9d^2)) = ((xa^3 - 4yb^3)/(xc^3 - 5yd^3))^(1/3)`
If x, y, z are in continued proportion prove that `(x + y)^2/(y + z)^2 = x/z`
If a, b, c and dare in continued proportion, then prove that
(a+ d)(b+ c)-(a+ c)(b+ d)= (b-c)2
If a, b, c are in continued proportion and a(b – c) = 2b, prove that: `a - c = (2(a + b))/a`.
If `x/a = y/b = z/c`, prove that `x^3/a^2 + y^2/b^2 + z^3/c^2 = ((x + y + z)^3)/((a + b ++ c)^2)`.
If 24 workers can build a wall in 15 days, how many days will 8 workers take to build a similar wall?
If a, b, c, d are in continued proportion, prove that:
`((a -b)/c + (a - c)/b)^2 - ((d - b)/c + (d - c)/b)^2 = (a - d)^2 (1/c^2 - 1/b^2)`
Choose the correct answer from the given options :
The fourth proportional to 3, 4, 5 is
The shadow of a 3 m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24 m long, how tall is the flagstaff?
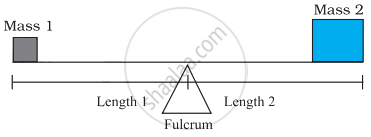
Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down.
Unequal masses will balance when the following proportion is true:
`("mass"1)/("length"2) = ("mass"2)/("length"1)`
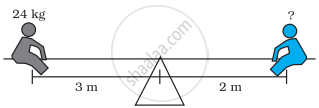
Two children can be balanced on a seesaw when
`("mass"1)/("length"2) = ("mass"2)/("length"1)`. The child on the left and child on the right are balanced. What is the mass of the child on the right?