Advertisements
Advertisements
प्रश्न
A train starting from stationary position and moving with uniform acceleration attains a speed of 36 km per hour in 10 minutes. Find its acceleration.
उत्तर
Initial velocity, u=0m/s
Final velocity, v=36km/h=10m/s
Time, t=10min =10 x 60=600 sec
Average velocity =
`"Inition velocity + Final velocity"/"2"`
Thats is, Average velocity= `(u+v)/2`
Also, Distance travelled= Average velocity ×Time
so, s=`((u+v))/2` × t ...............(1)
Form the first equation of motion, we have, v =u+at.
put this value of v in equation (1), we get:
s =`((u+u+at))/2 × t`
or s=`((2u+at)×t)/2`
or s = `(2ut+at^2)/2`
or s = `ut + 1/2 at^2`
where, s =distance travelledby the boby in time t
u= initial velocity of the body
and a= acceleration
Acceleration = `"Final velocity - Initial velocity"/"time taken"`
so, a= `(v-u)/t=( 10-0)/600 =10/600"m//s^2 =1/60m//s^s = 0.016m//s^2`
APPEARS IN
संबंधित प्रश्न
Give one example of a situation in which a body has a certain average speed but its average velocity is zero.
Fill in the following blank with suitable word :
A motorcycle has a steady……………. of 3 m/s2. This means that every………………. its…………….. increases by………….
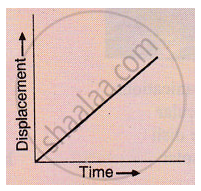
What conclusion can you draw about the velocity of a body from the displacement-time graph shown below :
A bus running at a speed of 18 km/h is stopped in 2.5 seconds by applying brakes. Calculate the retardation produced.
A train travelling at 20 m s-1 accelerates at 0.5 m s-2 for 30 s. How far will it travel in this time ?
A body starts from rest and acquires a velocity 10 m s-1 in 2 s. Find the acceleration.
Write three equations of uniformly accelerated motion relating the initial velocity (u), final velocity (v), time (t), acceleration (a) and displacement (S).
A body, initially at rest, starts moving with a constant acceleration 2 m s-2. Calculate: (i) the velocity acquired and (ii) the distance travelled in 5 s.
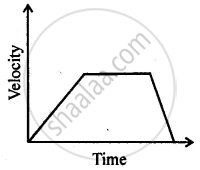
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
Two stones are thrown vertically upwards simultaneously with their initial velocities u1 and u2 respectively. Prove that the heights reached by them would be in the ratio of `"u"_1^2 : "u"_2^2` (Assume upward acceleration is –g and downward acceleration to be +g)
