Advertisements
Advertisements
प्रश्न
A uniform conducting wire of length 12a and resistance R is wound up as a current-carrying coil in the shape of (i) an equilateral triangle of side a; (ii) a square of sides a and, (iii) a regular hexagon of sides a. The coil is connected to a voltage source V0. Find the magnetic moment of the coils in each case.
उत्तर
In this problem, different shapes form figures of different area and the number of loops in each case is different hence, their magnetic moments varies.
Magnetic moment is m = nlA.
Since, the same wire is used in three cases with the same potentials, therefore, same current flows in three cases.
(i) For an equilateral triangle of side a,
As the total wire of length = 12a, so, the no. of loops n = `(12a)/(3a)` = 4
Magnetic moment of the coils m = nlA
As area of triangle is A = `sqrt(3)/4 a^2`
= `4I (sqrt(3)/4 a^2)`
∴ m = `Ia^2 sqrt(3)`
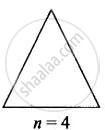
(ii) For a square of sides a,
A = a2
No. of loops n = `(12a)/(4a)` = 3
Magnetic moment of the coils m = nlA - `3I(a^2) = 3Ia^2`

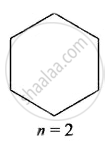
(iii) For a regular hexagon of sides a,
No. of loops n = `(12a)/(6a)` = 2
Area, A = `(6sqrt(3))/4 a^2`
Magnetic moment of the coils m = nlA
⇒ m = `2I((6sqrt(3))/4 a^2)`
⇒ m = `3sqrt(3)a^2I`, m is in a geometric series.
APPEARS IN
संबंधित प्रश्न
A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
Suppose that the radius of cross-section of the wire used in the previous problem is r. Find the increase in the radius of the loop if the magnetic field is switched off. Young's modulus of the material of the wire is Y.
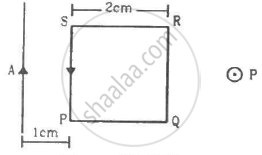
A square loop PQRS carrying a current of 6.0 A is placed near a long wire carrying 10 A as shown in figure. (a) Show that the magnetic force acting on the part PQ is equal and opposite to the part RS. (b) Find the magnetic force on the square loop.
A moving coil galvanometer has been fitted with a rectangular coil having 50 turns and dimensions 5 cm × 3 cm. The radial magnetic field in which the coil is suspended is of 0.05 Wb/m2. The torsional constant of the spring is 1.5 × 10−9 Nm/degree. Obtain the current required to be passed through the galvanometer so as to produce a deflection of 30°.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
A rectangular coil has 200 turns each of area 50 cm2 . It is capable of rotation about an axis joining the mid points of two opposite sides. When a current of 10 A is passed through it while its plane is at right angles to a uniform magnetic field, it experiences a torque of 5 Nm. The magnetic field will be ____________.
Two galvanometers 'G1' and 'G2' require 2 mA and 3 mA respectively to produce the same deflection. Then _______.
If number of turns in moving coil galvanometer becomes half, then the deflection for the same current will become ____________.
A current of 10 A is flowing in a wire of length 1.5 m. A force of 15 N acts on it when it is placed in a uniform magnetic field of 2 T. The angle between the magnetic field and the direction of the current is ______.
Calculate the orbital magnetic dipole moment of the electron in the second Bohr orbit of the hydrogen atom, given the radius of the orbit is 2.1 Å and the orbital speed is 1.1 × 106 m/s.
