Advertisements
Advertisements
प्रश्न
A wheel starting from rest is uniformly accelerated at 4 rad/s2 for 10 seconds. It is allowed to rotate uniformly for the next 10 seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
उत्तर
It is given that the area under the \[\omega - t\] curve gives the total angular displacement.
∴ Maximum angular velocity = \[\omega = \alpha t\]
\[\omega = 4 \times 10 = 40\text{ rad/s}\]
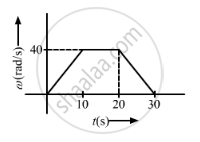
Area under the curve
\[= \frac{1}{2} \times 10 \times 40 + 40 \times 10 + \frac{1}{2} \times 40 \times 10\]
\[ = 800\text{ rad}\]
∴ Total angle rotated in 30 s = 800 rad.
APPEARS IN
संबंधित प्रश्न
In a rotating body, \[\alpha = \alpha r\text{ and }\nu = \omega r.\] Thus \[\frac{\alpha}{\alpha} = \frac{\nu}{\omega}.\] Can you use the theorems of ration and proportion studied in algebra so as to write \[\frac{\alpha + \alpha}{\alpha - \alpha} = \frac{\nu + \omega}{\nu - \omega}\]
Consider the following two equations
(A) \[L = I \omega\]
(B) \[\frac{dL}{dt} = \Gamma\]
In noninertial frames _______________ .
A wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, it reaches 100 rev/sec in 4 seconds. Find the angular acceleration. Find the angle rotated during these four seconds.
A body rotates about a fixed axis with an angular acceleration of one radian/second. Through what angle does it rotate during the time in which its angular velocity increases from 5 rad/s to 15 rad/s.
A hollow sphere of radius R lies on a smooth horizontal surface. It is pulled by a horizontal force acting tangentially from the highest point. Find the distance travelled by the sphere during the time it makes one full rotation.
