Advertisements
Advertisements
प्रश्न
A hollow sphere of radius R lies on a smooth horizontal surface. It is pulled by a horizontal force acting tangentially from the highest point. Find the distance travelled by the sphere during the time it makes one full rotation.
उत्तर
Let M be the mass of the hollow sphere and α be the angular acceleration produced in the sphere by the tangential force F.
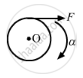
Torque due to this force,
\[\tau = F \times R\]
Also, \[\tau = I\alpha\]
\[\text{So, }F \times R = \left( \frac{2}{3} \right)M R^2 \alpha\]
\[ \Rightarrow \alpha = \frac{3F}{2MR}\]
Applying \[\theta = \omega_0 t + \frac{1}{2}\alpha t^2, \] we get
\[2\pi = \frac{1}{2}\alpha t^2 \]
\[ \Rightarrow t^2 = \frac{8\pi MR}{3F}\]
Let d be the distance travelled in this time t.
Acceleration,
\[a = \frac{F}{M}\]
\[\therefore d = \frac{1}{2}a t^2 \]
\[ = \frac{1}{2} \times \frac{F}{M} \times \left( \frac{8\pi MR}{3F} \right)\]
\[ = \frac{4\pi R}{3}\]
APPEARS IN
संबंधित प्रश्न
In a rotating body, \[\alpha = \alpha r\text{ and }\nu = \omega r.\] Thus \[\frac{\alpha}{\alpha} = \frac{\nu}{\omega}.\] Can you use the theorems of ration and proportion studied in algebra so as to write \[\frac{\alpha + \alpha}{\alpha - \alpha} = \frac{\nu + \omega}{\nu - \omega}\]
Consider the following two equations
(A) \[L = I \omega\]
(B) \[\frac{dL}{dt} = \Gamma\]
In noninertial frames _______________ .
A wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, it reaches 100 rev/sec in 4 seconds. Find the angular acceleration. Find the angle rotated during these four seconds.
A wheel starting from rest is uniformly accelerated at 4 rad/s2 for 10 seconds. It is allowed to rotate uniformly for the next 10 seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
A body rotates about a fixed axis with an angular acceleration of one radian/second. Through what angle does it rotate during the time in which its angular velocity increases from 5 rad/s to 15 rad/s.
