Question

A hollow sphere of radius R lies on a smooth horizontal surface. It is pulled by a horizontal force acting tangentially from the highest point. Find the distance travelled by the sphere during the time it makes one full rotation.

Answer 1

Let M be the mass of the hollow sphere and α be the angular acceleration produced in the sphere by the tangential force F.

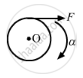
Torque due to this force,

\[\tau = F \times R\]

Also, \[\tau = I\alpha\]

\[\text{So, }F \times R = \left( \frac{2}{3} \right)M R^2 \alpha\]

\[ \Rightarrow \alpha = \frac{3F}{2MR}\]

Applying \[\theta =  \omega_0 t + \frac{1}{2}\alpha t^2, \] we get

\[2\pi = \frac{1}{2}\alpha t^2 \]

\[ \Rightarrow  t^2  = \frac{8\pi MR}{3F}\]

Let d be the distance travelled in this time t.

Acceleration,

\[a = \frac{F}{M}\]

\[\therefore   d = \frac{1}{2}a t^2 \]

\[ =   \frac{1}{2} \times \frac{F}{M} \times \left( \frac{8\pi MR}{3F} \right)\]

\[ = \frac{4\pi R}{3}\]