Advertisements
Advertisements
प्रश्न
एका कारखान्यातील कुशल आणि अकुशल कामगारांच्या रोजगारांचे गुणोत्तर 5 : 3 आहे. एका कुशल आणि एका अकुशल कामगाराचा एका दिवसाचा एकूण रोजगार 720 रुपये आहे, तर प्रत्येक कुशल कामगाराचा आणि अकुशल कामगाराचा रोजगार काढा.
उत्तर
समजा, कुशल कामगाराचा रोजगार ₹ x व अकुशल कामगाराचा रोजगार ₹ y आहे.
दिलेल्या पहिल्या अटीनुसार, कुशल आणि अकुशल कामगारांच्या रोजगारांचे गुणोत्तर 5 : 3 आहे.
`x/y = 5/3`
∴ 3x = 5y
∴ 3x - 5y = 0 ....(i)
दिलेल्या दुसऱ्या अटीनुसार, दोघांचा एका दिवसाचा पगार 720 रुपये आहे.
x + y = 720
∴ 5x + 5y = 3600 ...(ii) [दोन्ही बाजूंना 5 ने गुणून]
समीकरण (i) व (ii) ची बेरीज करून,
3x - 5y = 0
+ 5x + 5y = 3600
8x = 3600
∴ x = `3600/8` = 450
x = 450 ही किंमत समीकरण (i) मध्ये ठेवून,
3x - 5y = 0
3(450) - 5y = 0
∴ 1350 = 5y
∴ y = `1350/5` = 270
∴ कुशल कामगाराचा रोजगार ₹ 450, तर अकुशल कामगाराचा रोजगार ₹ 270 आहे.
APPEARS IN
संबंधित प्रश्न
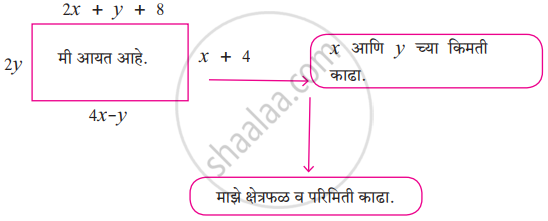
कृती पूर्ण करा.
विशालने 1900 किमी प्रवासापैकी काही अंतर बसने, तर उरलेले अंतर विमानाने पूर्ण केले. बसचा सरासरी वेग 60 किमी दर तास आहे, तर विमानाचा सरासरी वेग 700 किमी/तास आहे. जर हा प्रवास त्याने 5 तासांत पूर्ण केला असेल, तर विशालने बसने किती किमी प्रवास केला?
कांताबाईंनी दुकानातून दीड किलो चहा व पाच किलो साखर आणली. दुकानात जाऊन येण्यासाठी त्यांना 50 रुपये रिक्षाभाडे द्यावे लागले. यासाठी त्यांचे 700 रुपये खर्च झाले. नंतर त्यांना असे समजले, की या वस्तू ऑनलाइन ऑर्डर नोंदवून त्याच दराने घरपोच मिळतात. पुढील महिन्यात त्यांनी 2 किलोग्राम चहा व ७ किलोग्राम साखर ऑनलाइन मागवली, तेव्हा त्यांचा 880 रुपये खर्च झाला, तर चहा आणि साखर यांचा प्रतिकिलोग्राम दर काढा.

समीकरणे सोडवून उत्तर लिहा.
100 रुपयांच्या नोटांची संख्या `square` 50 रुपयांच्या नोटांची संख्या `square`
एका सरळ रस्त्यावर A आणि B ही दोन ठिकाणे आहेत. त्यांतील अंतर ३० किमी आहे. हमीद मोटारसायकलने A पासून B च्या दिशेने जाण्यास निघतो. त्याच वेळी जोसेफ मोटारसायकलने B पासून A च्या दिशेने जाण्यास निघतो. ते दोघे २० मिनिटांत एकमेकांना भेटतात. जोसेफ जर त्याच वेळी निघून विरुद्ध दिशेने गेला असता, तर त्याला हमीद तीन तासांनी भेटला असता, तर प्रत्येकाचा प्रवासाचा वेग किती होता?
समीकरण 3x - 2y = 17 मध्ये (i) y = -1 असताना x ची किंमत शोधा. (ii) x = 3 असताना y ची किंमत काढा.
सोडवा. 0.4x + 0.3y = 1.7; 0.7x – 0.2y = 0.8.
मी 75 ही संख्या मनात धरली, त्या संख्येच्या दोन्ही अंकांतील संबंध दर्शवणारी अट लिहा. मूळ संख्या आणि अंकांची अदलाबदल करून येणाऱ्या संख्येतील संबंध दर्शवणारी अट लिहा.
कोणतीही दोन एकसामयिक समीकरणे लिहा- ज्यामध्ये चलांच्या किमती 12 आणि 10 असतील.
एका समद्विभुज त्रिकोणाची परिमिती 24 सेमी आहे. एकरूप बाजूंची लांबी ही पायाच्या दुपटीपेक्षा 13 सेमीने कमी आहे, तर त्या त्रिकोणाच्या सर्व बाजूंची लांबी काढा.
