Advertisements
Advertisements
प्रश्न
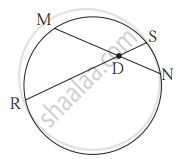
आकृती मध्ये, जीवा MN आणि RS एकमेकींना बिंदू D मध्ये छेदतात.
(1) जर RD = 15, DS = 4, MD = 8 तर DN = किती?
(2) जर RS = 18, MD = 9, DN = 8 तर DS = किती?
उत्तर
(1) जीवा MN व RS एकमेकांना वर्तुळाच्या अंतर्भागात बिंदू D मध्ये छेदतात. ....[पक्ष]
∴ MD × DN = RD × DS ....[जीवांच्या अंतर्छेदनाचे प्रमेय]
∴ 8 × DN = 15 × 4
∴ DN = `(15 xx 4)/8`
∴ DN = 7.5 एकक
(2) समजा, RD = x मानू.
RS = RD + DS .....[R - D - S]
∴ 18 = x + DS
∴ DS = 18 - x
आता, MD × DN = RD × DS ....[जीवांच्या अंतर्छेदनाचे प्रमेय]
∴ 9 × 8 = x(18 - x)
∴ 72 = 18x - x2
∴ x2 - 18x + 72 = 0
∴ x2 - 12x - 6x + 72 = 0
∴ x(x - 12) - 6 (x - 12) = 0
∴ (x - 12) (x - 6) = 0
∴ x - 12 = 0 किंवा x - 6 = 0
∴ x = 12 किंवा x = 6
∴ DS = 18 - 12 किंवा DS = 18 - 6
∴ DS = 6 एकक किंवा DS = 12 एकक
APPEARS IN
संबंधित प्रश्न
एका वर्तुळाच्या जीवा AB आणि CD परस्परांना वर्तुळाच्या अंतर्भागात बिंदू E मध्ये छेदतात. जर (AE) = 5.6, (EB) = 10, (CE) = 8 तर (ED) = किती?
आकृती मध्ये, m(कंस WY) = 44°, m(कंस ZX) = 68°, तर ∠ZTX चे माप ठरवा.
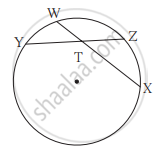
आकृती मध्ये, m(कंस WY) = 44°, m(कंस ZX) = 68°, तर WT = 4.8, TX = 8.0, YT = 6.4 तर TZ = किती?

आकृती मध्ये, m(कंस WY) = 44°, m(कंस ZX) = 68°, तर WX = 25, YT = 8, YZ = 26, तर WT = किती?

एका वर्तुळाच्या जीवा AB आणि जीवा CD परस्परांना वर्तुळाच्या अंतर्भागात बिंदू E मध्ये छेदतात. जर AE = 4, EB = 10, CE = 8, तर ED = किती?
3 सेमी त्रिज्या असलेल्या वर्तुळातील सर्वांत मोठ्या जीवेची लांबी किती?
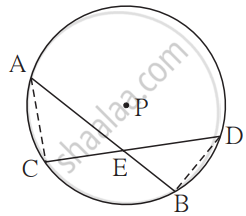
पक्ष:
केंद्र P असलेल्या वर्तुळाच्या जीवा AB आणि जीवा CD वर्तुळाच्या अंतर्भागात बिंदू E मध्ये छेदतात.
साध्य:
AE × EB = CE × ED
रचना:
रेख AC आणि रेख BD काढले.
रिकाम्या जागा भरून सिद्धता पूर्ण करा.
सिद्धता:
Δ CAE आणि Δ BDE मध्ये,
∠AEC ≅ ∠DEB ...`square`
`square` ≅ ∠BDE ...(एकाच वर्तुळकंसात अंतर्लिखित कोन)
∴ Δ CAE ~ Δ BDE ...`square`
∴ `square/ ("DE") = ("CE")/square` ...`square`
∴ AE × EB = CE × ED
