Advertisements
Advertisements
प्रश्न
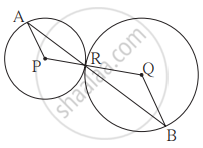
आकृती मध्ये, केंद्र P आणि Q असलेली वर्तुळे परस्परांना बिंदू R मध्ये स्पर्श करतात. बिंदू R मधून जाणारी रेषा त्या वर्तुळांना अनुक्रमे बिंदू A व बिंदू B मध्ये छेदते. तर -
(1) रेख AP || रेख BQ हे सिद्ध करा.
(2) ΔAPR ~ ΔRQB हे सिद्ध करा.
(3) जर ∠PAR चे माप 35° असेल, तर ∠RQB चे माप ठरवा.
उत्तर
केंद्र P आणि Q असलेली वर्तुळे परस्परांना बिंदू R मध्ये स्पर्श करतात.
∴ स्पर्शवर्तुळांच्या प्रमेयानुसार,
P-R-Q
(1) ΔPAR मध्ये,
रेख PA = रेख PR ..........[एकाच वर्तुळाच्या त्रिज्या]
∴ ∠PRA ≅ ∠PAR ...(i) [समद्विभुज त्रिकोणाचे प्रमेय]
त्याचप्रमाणे, ΔQBR मध्ये,
रेख QR = रेख QB .........[एकाच वर्तुळाच्या त्रिज्या]
∴ ∠RBQ ≅ ∠QRB .....(ii) [समद्विभुज त्रिकोणाचे प्रमेय]
परंतु, ∠PRA ≅ ∠QRB ......(iii) [विरुद्ध कोन]
∴ ∠PAR ≅ ∠RBQ ....(iv) [(i) व (ii) वरून]
परंतु, वरील कोन AB ही छेदिका असता, रेख AP व रेख BQ वरील व्युत्क्रम कोन आहेत.
∴ रेख AP || रेख BQ .....[व्युत्क्रम कोन कसोटी]
(2) ΔAPR व ΔRQB मध्ये,
∠PAR ≅ ∠QRB ....[(i) व (iii) वरून]
∠APR ≅ ∠RQB .....[व्युत्क्रम कोन]
∴ ΔAPR ∼ ΔRQB .....[समरूपतेच्या कोको कसोटीनुसार]
(3) ∠PAR = 35° ....[पक्ष]
∠RBQ = ∠PAR = 35° [(iv) वरून]
ΔRQB मध्ये,
∠RQB + ∠RBQ + ∠QRB = 180° ......[त्रिकोणाच्या कोनांच्या मापांची बेरीज 180° असते.]
∴ ∠RQB + ∠RBQ + ∠RBQ = 180° ....[(ii) वरून]
∴ ∠RQB + 2∠RBQ = 180°
∴ ∠RQB + 2 × 35° = 180°
∴ ∠RQB + 70° = 180°
∴ ∠RQB = 110°
APPEARS IN
संबंधित प्रश्न
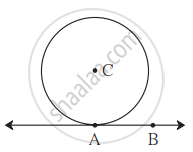
सोबतच्या आकृतीत, केंद्र C असलेल्या वर्तुळाची त्रिज्या 6 सेमी आहे. रेषा AB या वर्तुळाला बिंदू A मध्ये स्पर्श करते. या माहितीवरून खालील प्रश्नांची उत्तरे द्या.
(1) ∠CAB चे माप किती अंश आहे? का?
(2) बिंदू C हा रेषा AB पासून किती अंतरावर आहे? का?
(3) जर d(A,B) = 6 सेमी, तर d(B,C) काढा.
(4) ∠ABC चे माप किती अंश आहे? का?
त्रिज्या 4.5 सेमी असलेल्या वर्तुळाच्या दोन स्पर्शिका परस्परांना समांतर आहेत. तर त्या स्पर्शिकांतील अंतर किती हे सकारण लिहा.
बिंदू O केंद्र असलेल्या वर्तुळाला रेषा l बिंदू P मध्ये स्पर्श करते. जर वर्तुळाची त्रिज्या 9 सेमी असेल, तर खालील प्रश्नांची उत्तरे लिहा.
(1) d(O, P) = किती? का?
(2) जर d(O, Q) = 8 सेमी असेल. तर बिंदू Q चे स्थान कोठे असेल?
(3) d(O, R)=15 सेमी असेल तर बिंदू R ची किती स्थाने रेषा l वर असतील? ते बिंदू P किती अंतरावर असतील?

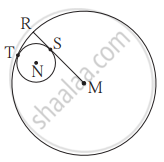
आकृती मध्ये, केंद्र N असलेले वर्तुळ केंद्र M असणाऱ्या वर्तुळाला बिंदू T मध्ये स्पर्श करते. मोठ्या वर्तुळाची त्रिज्या लहान वर्तुळाला बिंदू S मध्ये स्पर्श करते. जर मोठ्या व लहान वर्तुळांच्या त्रिज्या अनुक्रमे 9 सेमी व 2.5 सेमी असतील तर खालील प्रश्नांची उत्तरे शोधा आणि त्यांवरून MS : SR हे गुणोत्तर काढा.
(1) MT = किती?
(2) MN = किती?
(3) ∠NSM = किती?
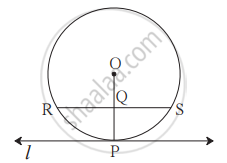
शेजारील आकृतीत, रेषा l ही केंद्र O असलेल्या वर्तुळाला बिंदू P मध्ये स्पर्श करते. बिंदू Q हा त्रिज्या OP चा मध्यबिंदू आहे. बिंदू Q ला सामावणारी जीवा RS || रेषा l. जर RS 12 सेमी असेल, तर वर्तुळाची त्रिज्या काढा.
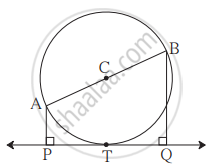
आकृती मध्ये, केंद्र C असलेल्या वर्तुळाचा रेख AB हा व्यास आहे. वर्तुळाची स्पर्शिका PQ वर्तुळाला बिंदू T मध्ये स्पर्श करते. रेख AP ⊥ रेषा PQ आणि रेख BQ ⊥ रेषा PQ. तर सिद्ध करा - रेख CP ≅ रेख CQ.
वर्तुळाच्या बाह्यभागातील बिंदूपासून त्या वर्तुळाला काढलेले स्पर्शिकाखंड एकरूप असतात हे प्रमेय सिद्ध करण्यासाठी आकृतीच्या आधारे खालील कृती पूर्ण करा.
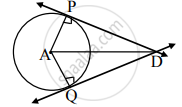
पक्ष: `square`
साध्य: `square`
सिद्धता:
त्रिज्या AP आणि AQ काढून प्रमेयाची खाली दिलेली सिद्धता रिकाम्या जागा भरून पूर्ण करा.
ΔPAD आणि ΔQAD यांमध्ये,
बाजू PA ≅ बाजू `square` ...........[एकाच वर्तुळाच्या त्रिज्या]
बाजू AD ≅ बाजू AD ...............[`square`]
∠APD ≅ ∠AQD = 90° ............[स्पर्शिका-त्रिज्या प्रमेय]
∴ ΔPAD ≅ ΔQAD ..................[`square`]
∴ बाजू DP ≅ बाजू DQ ...............[`square`]
आकृतीत रेख RM आणि रेख RN हे केंद्र O असलेल्या वर्तुळाचे स्पर्शिका खंड आहेत, तर रेख OR हा ∠MRN आणि ∠MON या दोन्ही कोनांचा दुभाजक आहे, हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
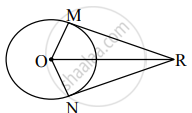
सिद्धता:
ΔRMO आणि ΔRNO यांमध्ये,
∠RMO ≅ ∠RNO = 90° ...............[`square`]
कर्ण OR ≅ कर्ण OR …..............[`square`]
बाजू OM ≅ बाजू [`square`] ..........…[एकाच वर्तुळाच्या त्रिज्या]
∴ ΔRMO ≅ ΔRNO ….......[`square`]
∠MOR ≅ ∠NOR
तसेच, ∠MRO ≅ [`square`] ......................[`square`]
∴ रेख OR ∠MRN आणि ∠MON या दोन्ही कोनांची दुभाजक आहे.
दिलेल्या आकृतीत, Q केंद्र असलेल्या वर्तुळाच्या रेख PM आणि PN स्पर्शिका आहेत. जर ∠MPN = 40°, तर ∠MQN चे माप काढा.
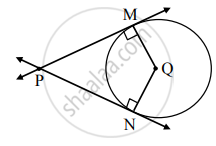
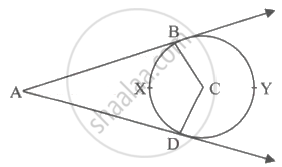
वरील आकृतीत, C केंद्र असलेल्या वर्तुळाला A या बाह्यबिंदूतून AB आणि AD हे स्पर्शिकाखंड काढले आहेत. तर सिद्ध करा:
∠A = `1/2` [m(कंस BYD) - m(कंस BXD)]
