Question

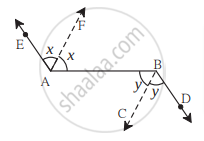
आकृती मध्ये किरण AE || किरण BD किरण AF हा ∠EAB चा आणि किरण BC हा ∠ABD चा दुभाजक आहे, तर सिद्ध करा की, रेषा AF || रेषा BC

Answer 1

AF हा ∠EAB चा आणि किरण BC हा ∠ABD चा दुभाजक आहे, म्हणून

∠EAF = ∠FAB = ∠x = `1/2`∠EAB आणि

∠CBA = ∠DBC = ∠y = `1/2`∠ABD

∴ ∠x = `1/2` ∠EAB आणि ∠y = `1/2`∠ABD     ...(1)

किरण AE पासून || किरण BD आणि रेख AB ही त्यांना A आणि B मध्ये छेदणारी छेदिका आहे.

∠EAB = ∠ABD     ...(आंतरव्युत्क्रम कोन)

दोन्ही बाजूंना `1/2` ने गुणून

`1/2`∠EAB = `1/2`∠ABD

∴ (1) वरून

∠x = ∠y   

परंतु, ∠x आणि ∠y हे किरण AF आणि किरण BC च्या आंतरव्युत्क्रम कोन आहेत व रेषा AB ही त्यांची छेदिका आहे.

∴ किरण AF || किरण BC   ...(व्युत्क्रम कोन कसोटी)