Advertisements
Advertisements
प्रश्न
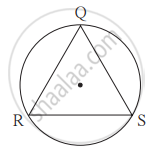
आकृती मध्ये ΔQRS समभुज आहे. तर दाखवा की -
(1) कंस RS ≅ कंस QS ≅ कंस QR
(2) कंस QRS चे माप 240° आहे.
उत्तर
i. ΔQRS हा समभुज त्रिकोण आहे. ......[पक्ष]
∴ रेख RS ≅ रेख QS ≅ रेख QR .....[समभुज त्रिकोणाच्या बाजू]
∴ कंस RS ≅ कंस QS ≅ कंस QR .....[एकाच वर्तुळाच्या एकरूप जीवांचे संगत कंस एकरूप असतात.]
ii. समजा, m(कंस RS) = m(कंस QS) = m(कंस QR) = x°
m(कंस RS) + m(कंस QS) + m(कंस QR) = 360° .....[वर्तुळाचे माप 360° असते, कंसांच्या मापांच्या बेरजेचा गुणधर्म]
∴ x + x + x = 360°
∴ 3x = 360°
∴ x = `360^circ/3` = 120°
∴ m(कंस RS) = m(कंस QS) = m(कंस QR) = 120° ....(i)
आता, m(कंस QRS) = m(कंस QR) + m(कंस RS) .....[कंसांच्या मापांच्या बेरजेचा गुणधर्म]
= 120° + 120° ....[(i) वरून]
∴ m(कंस QRS) = 240°
APPEARS IN
संबंधित प्रश्न
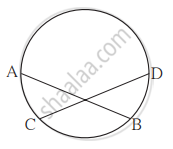
आकृती मध्ये, जीवा AB ≅ जीवा CD, तर सिद्ध करा - कंस AC ≅ कंस BD
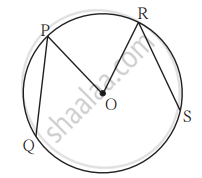
सोबतच्या आकृतीत, केंद्र O असलेल्या वर्तुळाच्या रेख PQ आणि रेख RS या एकरूप जीवा आहेत. जर ∠POR = 70° आणि m(कंस RS) = 80°, तर -
(1) m(कंस PR) किती?
(2) m(कंस QS) किती?
(3) m(कंस QSR) किती?
एकाच वर्तुळाच्या एकरूप कंसांच्या संगत जीवा एकरूप असतात हे प्रमेय रिकाम्या जागा भरून पूर्ण करा.
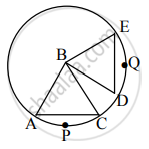
पक्ष : केंद्र B असलेल्या वर्तुळात कंस APC ≅ कंस DQE
साध्य : जीवा AC ≅ जीवा DE
सिद्धता : ΔABC आणि ΔDBE यांमध्ये,
बाजू AB ≅ बाजू DB ….........`square`
बाजू BC ≅ बाजू `square` ........`square`
∠ABC ≅ ∠DBE ...............[एकरूप कंसांची व्याख्या]
ΔABC ≅ ΔDBE .......................`square`
जीवा AC ≅ जीवा DE ..........[एकरूप त्रिकोणांच्या संगत बाजू]
'O' केंद्र असलेल्या वर्तुळाच्या जीवा AB व जीवा CD एकरूप आहेत. जर M(कंस AB) = 120°, तर M(कंस CD) काढा.
