Advertisements
Advertisements
प्रश्न
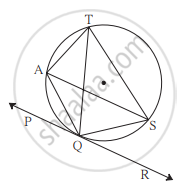
आकृती मध्ये रेषा PR वर्तुळाला बिंदू Q मध्ये स्पर्श करते. या आकृतीच्या आधारे खालील प्रश्नांची उत्तरे लिहा.
(1) ∠TAQ आणि ∠TSQ यांच्या मापांची बेरीज किती?
(2) ∠AQP शी एकरूप असणारे कोन कोणते?
(3) ∠QTS शी एकरूप असणारे कोन कोणते?
(4) जर ∠TAS = 65°, तर ∠TQS आणि कंस TS यांची मापे सांगा.
(5) जर ∠AQP = 42° आणि ∠SQR = 58°, तर ∠ATS चे माप काढा.
उत्तर
(1) `square`AQST हा चक्रीय चौकोन आहे. ....[पक्ष]
∴ ∠TAQ + ∠TSQ = 180° .....[चक्रीय चौकोनाचे संमुख कोन परस्परांचे पूरक कोन असतात.]
(2) रेषा PR ही स्पर्शिका आहे व रेख AQ ही छेदिका आहे. ......[पक्ष]
∴ ∠AQP = `1/2`m(कंस AQ) ......[स्पर्शिका-छेदिका कोनाचे प्रमेय]
परंतु, ∠ASQ = `1/2`m(कंस AQ) .....[अंतर्लिखित कोनाचे प्रमेय]
∴ ∠AQP ≅ ∠ASQ
त्याचप्रमाणे आपण सिद्ध करू शकतो, की
∠AQP ≅ ∠ATQ
(3) ∠QTS = `1/2`m(कंस QS) .....[अंतर्लिखित कोनाचे प्रमेय]
परंतु, ∠SQR = `1/2`m(कंस QS) ......[स्पर्शिका-छेदिका कोनाचे प्रमेय]
∴ ∠QTS ≅ ∠SQR
तसेच, ∠QTS = ∠QAS ...........[एकाच कंसातील अंतर्लिखित कोन]
(4) ∠TQS = ∠TAS .......[एकाच कंसातील अंतर्लिखित कोन]
∴ ∠TQS = 65°
आता, ∠TQS = `1/2`m(कंस TS) ......[अंतर्लिखित कोनाचे प्रमेय]
∴ 65° = `1/2`m(कंस TS)
∴ m(कंस TS) = 65° × 2
∴ m(कंस TS) = 130°
(5) ∠AQP + ∠AQS + ∠SQR = 180° .....[रेषीय जोडीतील कोन]
∴ 42° + ∠AQS + 58° = 180°
∴ ∠AQS + 100° = 180° ......(i)
परंतु, `square`AQST हा चक्रीय चौकोन आहे.
∴ ∠AQS + ∠ATS = 180° .....(ii) [चक्रीय चौकोनाचे प्रमेय]
∴ ∠ATS = 100° ......[(i) व (ii) वरून]
APPEARS IN
संबंधित प्रश्न
चक्रीय `square`MRPN मध्ये, ∠R = (5x - 13)° आणि ∠N = (4x + 4)°, तर ∠R आणि ∠N यांची मापे ठरवा.
प्रत्येक उपप्रश्नासाठी चार पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक पर्याय निवडा.
चक्रीय `square`ABCD मध्ये, कोन ∠A च्या मापाची दुप्पट ही ∠C च्या मापाच्या तिप्पटी एवढी आहे. तर ∠C चे माप किती?
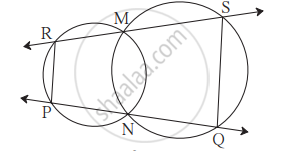
आकृती मध्ये, दोन वर्तुळे एकमेकांना बिंदू M व N मध्ये छेदतात. बिंदू M व N मधून काढलेल्या वृत्तछेदिका बिंदू R व S मध्ये, आणि बिंदू P व Q मध्ये छेदतात. तर रेख PR || रेख QS, हे सिद्ध करा.
चक्रीय चौकोनाचा बाह्यकोन त्याच्या संलग्न कोनाच्या संमुख कोनाशी एकरूप असतो हे प्रमेय सिद्ध करण्यासाठी पुढील कृती पूर्ण करा.
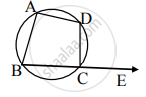
पक्ष: `square` ABCD चक्रीय चाकोन आहे.
`square` `square` ABCD चा बाह्यकोन आहे.
साध्य: ∠DCE ≅ ∠BAD
सिद्धता:
`square` + BCD = `square` ..........[रेषीय जोडीतील कोन] (i)
`square` ABCD चक्रीय चाकोन आहे.
`square` + ∠BAD = `square` ........[चक्रीय चौकोनाचे प्रमेय] (ii)
∴ (i) व (ii) वरून
∠DCE ≅ ∠BCD = `square` + ∠BAD
∠DCE ≅ ∠BAD
खालील प्रमेय सिद्ध करा:
चक्रीय चाकौनाचे संमुख कोन परस्परांचे पूरककोन असतात.
आकृतीमध्ये, `square`PQRS हा चक्रीय चौकोन आहे. बाजू PQ ≅ बाजू RQ, ∠PSR = 110°, तर ∠PQR = किती?
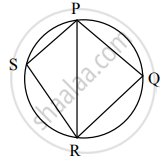
सिद्ध करा 'चक्रीय चौकोनाचे संमुख कोन परस्परांचे पूरककोन असतात.'
