Advertisements
Advertisements
प्रश्न
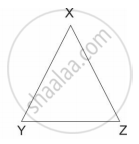
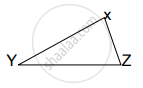
आकृती मध्ये रेख XY || रेख BC तर खालील पैकी कोणते विधान सत्य आहे?
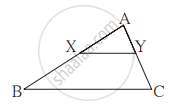
विकल्प
`"AB"/"AC" = "AX"/"AY"`
`"AX"/"XB" = "AY"/"AC"`
`"AX"/"YC" = "AY"/"XB"`
`"AB"/"YC" = "AC"/"XB"`
उत्तर
रेख XY || रेख BC तर सत्य विधान `"AB"/"AC" = "AX"/"AY"` हे आहे.
सपष्टीकरण :
ΔABC ∼ ΔAXY ....…[समरूपतेची कोको कसोटी]
∴ `"AB"/"AX" = "AC"/"AY"` ...[समरूप त्रिकोणांच्या संगत बाजू]
∴ `"AB"/"AC" = "AX"/"AY"` .....[एकांतर क्रियेने]
APPEARS IN
संबंधित प्रश्न
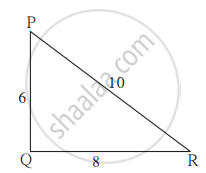
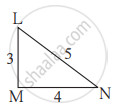
आकृती मधील त्रिकोण समरूप आहेत का? असतील तर कोणत्या कसोटीनुसार?
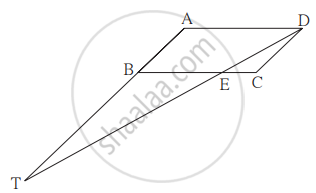
`square"ABCD"` हा समांतरभुज चौकोन आहे. बाजू BC वर E हा एक बिंदू आहे, रेषा DE ही किरण AB ला T बिंदूत छेदते. तर DE × BE = CE × TE दाखवा.
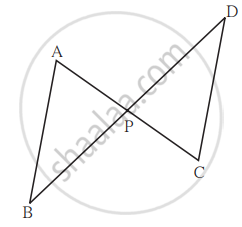
आकृतीत रेख AC व रेख BD परस्परांना P बिंदूत छेदतात आणि `"AP"/"CP" = "BP"/"DP"` तर सिद्ध करा, ΔABP ∼ ΔCDP.
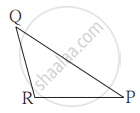
जर ΔABC व ΔPQR मध्ये एका एकास एक संगतीत `"AB"/"QR" = "BC"/"PR" = "CA"/"PQ"` तर खालीलपैकी सत्य विधान कोणते?

आकृती मध्ये XY || बाजू AC. जर 2AX = 3BX आणि XY = 9 तर AC ची किंमत काढण्यासाठी खालील कृती पूर्ण करा.

कृती : 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX" + "BX")/"BX" = (square + square)/square` ......(योग क्रिया करून)
`"AB"/"BX" = square/square` ......(I)
ΔBCA ~ ΔBYX .......(समरूपतेची `square` कसोटी)
∴ `"BA"/"BX" = "AC"/"XY"` ..........(समरूप त्रिकोणाच्या संगत बाजू)
∴ `square/square = "AC"/9`
∴ AC = `square` ..........(I) वरून
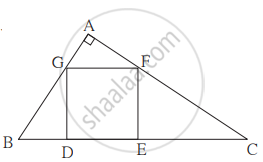
ΔABC मध्ये ∠A = 90°. `square`DEFG या चौरसाचे D व E हे शिरोबिंदू बाजू BC वर आहेत. बिंदू F हा बाजू AC वर आणि बिंदू G हा बाजू AB वर आहे. तर सिद्ध करा. DE2 = BD × EC (ΔGBD व ΔCFE हे समरूप दाखवा. GD = FE = DE याचा उपयोग करा.)
∆DEF व ∆XYZ मध्ये `"DE"/"XY" = "FE"/"YZ"` आणि ∠E ≅ ∠Y, तर ∆DEF व ∆∆XYZ हे कोणत्या कसोटीनुसार समरूप होतील?

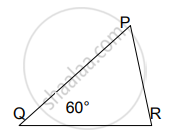
आकृतीचे निरीक्षण करून त्रिकोण समरूप आहेत का ते ठरवा. असल्यास समरूपता कसोटी लिहा. ∠P = 35°, ∠X = 35° व ∠Q = 60°, ∠Y = 60°

वरील आकृतीत रेख AC आणि रेख BD परस्परांना P बिंदूत छेदतात. जर `"AP"/"CP" = "BP"/"DP"` तर ΔABP ∼ ΔCDP दाखवण्यासाठी खालील कृती पूर्ण करा.
कृती: ΔABP व ΔCDP मध्ये
`"AP"/"CP" = "BP"/"DP" ....square`
∠APB ≅ `square` ...... विरुद्ध कोन
∴ `square` ∼ ΔCDP ....... समरूपतेची `square` कसोटी.

