Question

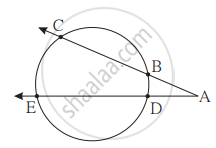
आकृति में,

(1) m(चाप CE) = 54°, m(चाप BD) = 23°, तो ∠CAE = कितना? 

(2) AB = 4.2, BC = 5.4, AE = 12.0 तो AD = कितना?

(3) AB = 3.6, AC = 9.0, AD = 5.4 तो AE = कितना?

 

Answer 1

(1) m(चाप CE) = 54°, m(चाप BD) = 23° ............(दिया है |) 

∠CAE का शीर्षबिंदु, वृत्त के बाह्य भाग में है और कोण द्वारा चाप CE और चाप BD अंतःखंडित होता है |

∴ ∠CAE = `1/2 xx` [m(चाप CE) - m(चाप BD)]

∴ ∠CAE = `1/2 xx [54^circ - 23^circ]`

∴ ∠CAE = `1/2 xx [31^circ]`

∴ ∠CAE = 15.5°.

(2) AB = 4.2, BC = 5.4, AE = 12 ..............(दिया है |) 

AC = AB + BC ...........(A-B-C)

∴ AC = 4.2 + 5.4

∴ AC = 9.6

जीवा CB तथा जीवा ED, वृत्त के बाह्य भाग में बिंदु A पर प्रतिच्छेदित करते है |

∴ जीवाओं के बहिर्च्छेदन के प्रमेय से,

AB × AC = AD × AE

∴ `4.2 xx 9.6 = "AD" xx 12`

∴ AD = `(4.2 xx 9.6)/12`

∴ AD = `(4.2 xx 9.6 xx 100)/(12 xx 100)`

∴ AD = `(42 xx 96)/(12 xx 100)`

∴ AD = `336/100`

∴ AD = 3.36.

(3) AB = 3.6, AC = 9, AD = 5.4 ...........(दिया है |) 

जीवा CB तथा जीवा ED, वृत्त के बाह्य भाग में बिंदु A पर प्रतिच्छेदित करते है |

∴ जीवाओं के बहिर्च्छेदन के प्रमेय से,

AB × AC = AD × AE

∴ `3.6 xx 9 = 5.4 xx "AE"`

∴ AE = `(3.6 xx 9)/5.4`

∴ AE = `(3.6 xx 9 xx 10)/(5.4 xx 10)`

∴ AE = `(36 xx 9)/54`

∴ AE = 6.

(1) ∠CAE = 15.5°,

(2) AD = 3.36 और

(3) AE = 6.