Advertisements
Advertisements
प्रश्न
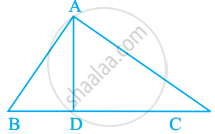
आकृति में, ∠BAC = 90° तथा AD ⊥ BC है।
इस आकृति में, समकोण त्रिभुजों की संख्या है -
विकल्प
1
2
3
4
उत्तर
3
स्पष्टीकरण:
एक त्रिभुज, जिसमें एक कोण 90° के बराबर होता है, उसे समकोण त्रिभुज कहा जाता है।
चूँकि, ∠BAC = 90°
ΔBAC एक समकोण त्रिभुज है।
इसके अलावा, ∠ADB = ∠ADC = 90° ...... [AD लंबवत BC के लिए]
∠ADB और ∠ADC भी समकोण त्रिभुज हैं।
इसलिए, 3 समकोण त्रिभुज हैं।
APPEARS IN
संबंधित प्रश्न
त्रिभुज ABC का एक रफ चित्र खींचिए। इस त्रिभुज के अभ्यंतर में एक बिंदु P अंकित कीजिए और उसके बहिर्भाग में एक बिंदु Q अंकित कीजिए। बिंदु A इसके अभ्यंतर में स्थित है या बहिर्भाग में स्थित है?
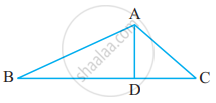
संलग्न आकृति में तीन त्रिभुजों की पहचान कीजिए।
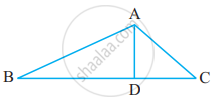
किन दो त्रिभुजों में कोण ∠B उभयनिष्ठ है?
एक त्रिभुज जिसकी सभी भुजाएँ असमान लम्बाइयों की हों, एक ______ त्रिभुज कहलाता है।
सभी समबाहु त्रिभुज समद्विबाहु भी होते हैं।
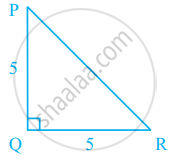
आकृति में, यदि PQ ⊥RQ, PQ = 5 cm और QR = 5 cm है, तब ΔPQR
निम्नलिखित आकृतियों (i) और (ii) में क्या समानता हैं?
 |
 |
| (i) | (ii) |
क्या आकृति (i) त्रिभुज है? यदि नहीं तो क्यों?
क्या हम ऐसे दो न्यूनकोण प्राप्त कर सकते हैं? जिनका योग एक न्यूनकोण हो? क्यों या क्यों नहीं?
क्या हम ऐसे दो न्यूनकोण प्राप्त कर सकते हैं? जिनका योग एक समकोण हो? क्यों या क्यों नहीं?
क्या हम ऐसे दो न्यूनकोण प्राप्त कर सकते हैं? जिनका योग एक प्रतिवर्ती कोण हो? क्यों या क्यों नहीं?
