Advertisements
Advertisements
प्रश्न
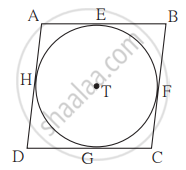
आकृति में, T केंद्र वाले वृत्त के चारों ओर समांतर `square` ABCD परिलिखित किया गया है | (अर्थात उस चतुर्भुज की चारों भुजाएँ वृत्त को स्पर्श करती हैं |) बिंदु E, F, G और H स्पर्श बिंदु है। यदि AE = 4.5 और EB = 5.5, तो AD का मान ज्ञात कीजिए ।
उत्तर
AE = 4.5 और EB = 5.5 ...(दिया है |)
AH = AE = 4.5
BF = BE = 5.5
मानो कि, DH = DG = x
CG = CF = y ...(स्पर्श रेखाखंड का प्रमेय)
`square` ABCD एक समांतर चतुर्भुज है| ...(दिया है |)
∴ AB = CD ...(समांतर चतुर्भुज की सम्मुख भुजाएँ)
∴ AE + EB = CG + GD ...(A-E-B और C-G-D)
∴ 4.5 + 5.5 = y + x
∴ x + y = 10 ...(1)
AD = BC ...(समांतर चतुर्भुज की सम्मुख भुजाएँ)
∴ AH + HD = BF + FC ...(A-H-D और B-F-C)
∴ 4.5 + x = 5.5 + y
∴ x - y = 5.5 - 4.5
∴ x - y = 1 ...(2)
(1) और (2) को जोड़ने पर,
x + y = 10
+ x - y = 1
2x = 11
∴ x = `11/2`
∴ x = 5.5
∴ DG = DH = 5.5
AD = AH + HD ...(A-H-D)
∴ AD = 4.5 + 5.5
∴ AD = 10
APPEARS IN
संबंधित प्रश्न
आकृति में, बिंदु ‘O’ वृत्त का केंद्र और रेख AB तथा रेख AC स्पर्शरेखाखंड हैं । यदि वृत्त की त्रिज्या r और AB = r हो, तो सिद्ध कीजिए कि, `square`ABOC एक वर्ग है |
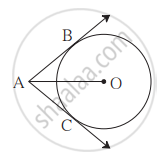
‘O’ केंद्रवाले वृत्त के बाह्य बिंदु ‘P’ से वृत्त पर स्थित बिंदु A से स्पर्श रेखा AP खींची गई है। OP = 12 सेमी तथा ∠OPA = 30° हो, तो वृत्त की त्रिज्या ______ होगी।
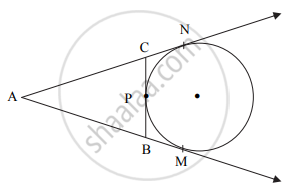
ΔABC में, भुजा BC को एक वृत्त बाह्यभाग में स्पर्श करता है। उसी प्रकार भुजा AC और भुजा AB को आगे बढ़ाने पर यह वृत्त को बिन्दु N तथा बिन्दु M पर स्पर्श करता है, तो सिद्ध कीजिए: AM = `1/2`(ΔABC की परिमिति)
