Advertisements
Advertisements
प्रश्न
ΔABC मध्ये, रेख AD ⊥ बाजू BC, रेख BE ⊥ बाजू AC, रेख CF ⊥ बाजू AB. बिंदू O हा शिरोलंबसंपात आहे. तर बिंदू O हा ΔDEF चा अंतर्मध्य होतो, हे सिद्ध करा.
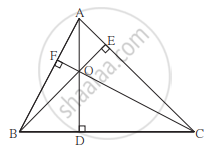
उत्तर
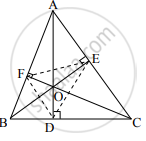
पक्ष: रेख AD ⊥ बाजू BC, रेख BE ⊥ बाजू AC, रेख CF ⊥ बाजू AB.
साध्य: बिंदू O हा ΔDEF चा अंतर्मध्य आहे.
रचना: DE, EF व DF काढा.
सिद्धता:
∠OFA = ∠OEA = 90° .....[पक्ष]
आता, ∠OFA + ∠OEA = 90° + 90°
∴ ∠OFA + ∠OEA = 180°
∴ `square`OFAE हा चक्रीय चौकोन आहे. .......[चक्रीय चौकोनाच्या प्रमेयाचा व्यत्यास]
∴ बिंदू O, F, A, E हे एका वर्तुळावर आहेत
∴ रेख OE तिच्या एकाच बाजूला ∠OFE व ∠OAE हे एकरूप कोन निश्चित करते.
∴ ∠OFE = ∠OAE ......(i)
∠OFB = ∠ODB = 90° .....[पक्ष]
आता, ∠OFB + ∠ODB = 90° + 90°
∴ ∠OFB + ∠ODB = 180°
∴ `square`OFBD हा चक्रीय चौकोन आहे. .......[चक्रीय चौकोनाच्या प्रमेयाचा व्यत्यास]
∴ बिंदू O, F, B, D हे एका वर्तुळावर आहेत
∴ रेख OD तिच्या एकाच बाजूला ∠OFD व ∠OBD हे एकरूप कोन निश्चित करते.
∴ ∠OFD = ∠OBD .....(ii)
ΔAEO व ΔBDO मध्ये,
∠AEO = ∠BDO .....[प्रत्येक कोनाचे माप 90° आहे.]
∠AOE = ∠BOD ......[विरुद्ध कोन]
∴ ΔAEO ∼ ΔBDO .....[समरूपतेची कोको कसोटी]
∴ ∠OAE = ∠OBD .....(iii) [समरूप त्रिकोणांचे संगत कोन]
∴ ∠OFE = ∠OFD ...........[(i), (ii) व (iii) वरून]
∴ किरण FO ∠EFD ला दुभागतो.
त्याचप्रमाणे आपण सिद्ध करू शकतो, की किरण EO व किरण DO हे अनुक्रमे ∠FED व ∠FDE ला दुभागतात.
∴ बिंदू O हा ΔDEF च्या ∠D, ∠E व ∠F च्या कोनदुभाजकांचा छेदनबिंदू आहे.
∴ बिंदू O हा ΔDEF चा अंतर्मध्य आहे.
APPEARS IN
संबंधित प्रश्न
कोणताही आयत हा चक्रीय चौकोन असतो हे सिद्ध करा.
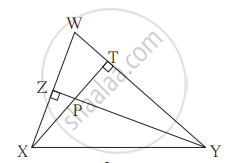
आकृती मध्ये, रेख YZ आणि रेख XT हे ΔWXY चे शिरोलंब बिंदू P मध्ये छेदतात तर सिद्ध करा,
(1) `square`WZPT हा चक्रीय आहे.
(2) बिंदू X, Z, T, Y एकाच वर्तुळावर आहेत.
चक्रीय `square`MRPN मध्ये, ∠R = (5x - 13)° आणि ∠N = (4x + 4)°, तर ∠R आणि ∠N यांची मापे काढण्यासाठी खालील कृती पूर्ण करा.
उकल:
`square`MRPN हा चक्रीय चौकोन आहे.
चक्रीय चौकोनाचे संमुख कोन परस्परांचे `square` असतात.
∠R + ∠N = `square`
∴ (5x - 13)° + (4x + 4)° = `square`
∴ 9x = 189
∴ x = `square`
∴ ∠R = (5x - 13)° = `square`
∴ ∠N = (4x + 4)° = `square`
