Advertisements
Advertisements
प्रश्न
दोन वर्तुळे परस्परांना बिंदू A व E मध्ये छेदतात. बिंदू E मधून काढलेली त्यांची सामाईक वृत्तछेदिका वर्तुळांना बिंदू B व D मध्ये छेदते. बिंदू B व D मधून काढलेल्या स्पर्शिका एकमेकींना बिंदू C मध्ये छेदतात. सिद्ध करा : `square`ABCD चक्रीय आहे.
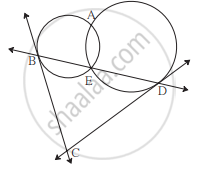
उत्तर
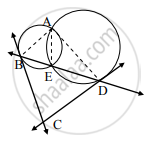
पक्ष: दोन वर्तुळे परस्परांना बिंदू A व E मध्ये छेदतात. रेख BC व रेख CD या वर्तुळाच्या स्पर्शिका आहेत.
साध्य: `square`ABCD चक्रीय आहे.
रचना: रेख AB, रेख AE व रेख AD काढा.
सिद्धता:
`{:(∠"EBC" = ∠"BAE"), (∠"EDC" = ∠"DAE"):}}` ......(i) (ii) [स्पर्शिका-छेदिका प्रमेय]
ΔBCD मध्ये,
∠DBC + ∠BDC + ∠BCD = 180° ......[त्रिकोणाच्या कोनांच्या मापांची बेरीज 180° असते.]
∴ ∠EBC + ∠EDC + ∠BCD = 180° ....(iii) [B-E-D]
∴ ∠BAE + ∠DAE + ∠BCD = 180° ....[(i), (ii), (iii) वरून]
∴ ∠BAD + ∠BCD = 180° ....[कोनांच्या बेरजेचा गुणधर्म]
∴ `square`ABCD चक्रीय आहे. .....[चक्रीय चौकोनाच्या प्रमेयाचा व्यत्यास]
APPEARS IN
संबंधित प्रश्न
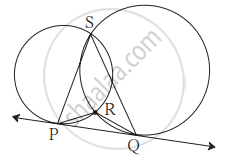
आकृती मध्ये दोन वर्तुळे परस्परांना बिंदू S व R मध्ये छेदतात. त्यांची रेषा PQ ही सामाईक स्पर्शिका त्यांना बिंदू P व Q मध्ये स्पर्श करते, तर सिद्ध करा - ∠PRQ + ∠PSQ = 180°
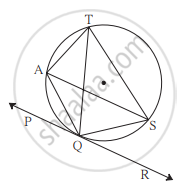
आकृती मध्ये रेषा PR वर्तुळाला बिंदू Q मध्ये स्पर्श करते. या आकृतीच्या आधारे खालील प्रश्नाचं उत्तर लिहा.
∠AQP शी एकरूप असणारे कोन कोणते?
जर sinθ = cosθ, तर θ चे माप किती?
