Advertisements
Advertisements
प्रश्न
ABCD एक समलंब है जिसमें AB || DC और ∠A = ∠B = 45° है। इस समलंब के कोण C और D ज्ञात कीजिए।
उत्तर
दिया गया है, ABCD एक समलंब है और आकृति में जिसकी समांतर भुजाएँ AB और DC हैं।
चूँकि AB || CD और BC एक तिर्यक रेखा है, तो दो सम्मुख कोणों का योग 180° होता है।
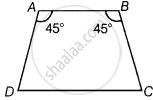
∴ ∠B + ∠C = 180º
⇒ ∠C = 180º – ∠B = 180º – 45º ...[∵ ∠B = 45º दिया गया है।]
⇒ ∠C = 135º
इसी प्रकार, ∠A + ∠D = 180º ...[सम्मिलन कोणों का योग 180º है।]
⇒ ∠D = 180º – 45º ...[∵ ∠A = 45º दिया गया है।]
⇒ ∠D = 135º
अत:, कोण C और D प्रत्येक 135º हैं।
APPEARS IN
संबंधित प्रश्न
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
- ABCD एक वर्ग है।
- विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
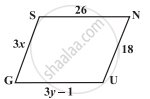
निम्न आकृति GUNS समांतर चतुर्भुज हैं। x तथा y ज्ञात कीजिए (लंबाई cm में है) :
निम्नलिखित के लिए कारण दीजिए:
वर्ग, आयत, समांतर चतुर्भुज और समचतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग एक समांतर चतुर्भुज भी है।
एक समांतर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लंबाई ज्ञात कीजिए।
∆ABC में, AB = 5 cm, BC = 8 cm और CA = 7 cm हैं। यदि D और E क्रमश : AB और BC के मध्य-बिंदु हैं, तो DE की लंबाई निर्धारित कीजिए।
एक समांतर चतुर्भुज MODE में, ∠M कोण ∠O के समद्विभाजक Q पर मिलते हैं। ∠MQO की माप ज्ञात कीजिए।
किसी समांतर चतुर्भुज का एक विकर्ण उसके एक कोण को समद्विभाजित करता है। क्या वह दूसरे कोण को भी समद्विभाजित करेगा? कारण दीजिए।
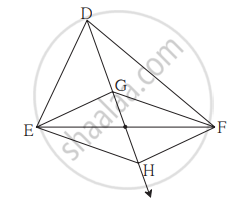
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।
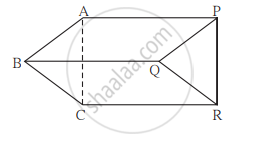
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR