Advertisements
Advertisements
Question
ABCD एक समलंब है जिसमें AB || DC और ∠A = ∠B = 45° है। इस समलंब के कोण C और D ज्ञात कीजिए।
Solution
दिया गया है, ABCD एक समलंब है और आकृति में जिसकी समांतर भुजाएँ AB और DC हैं।
चूँकि AB || CD और BC एक तिर्यक रेखा है, तो दो सम्मुख कोणों का योग 180° होता है।
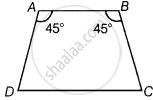
∴ ∠B + ∠C = 180º
⇒ ∠C = 180º – ∠B = 180º – 45º ...[∵ ∠B = 45º दिया गया है।]
⇒ ∠C = 135º
इसी प्रकार, ∠A + ∠D = 180º ...[सम्मिलन कोणों का योग 180º है।]
⇒ ∠D = 180º – 45º ...[∵ ∠A = 45º दिया गया है।]
⇒ ∠D = 135º
अत:, कोण C और D प्रत्येक 135º हैं।
APPEARS IN
RELATED QUESTIONS
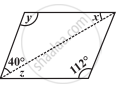
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:
एक चतुर्भुज की कच्ची आकृति खीचिए जो समांतर चतुर्भुज न हो परंतु जिसके दो सम्मुख कोणों के माप बराबर हों।
निम्नलिखित के लिए कारण दीजिए:
वर्ग एक समांतर चतुर्भुज भी है।
क्या किसी चतुर्भुज के सभी कोण न्यून कोण हो सकते हैं? अपने उत्तर का कारण दीजिए।
एक समांतर चतुर्भुज ABCD में, AB = 10 cm और AD = 6 cm है। ∠A का समद्विभाजक DC से E पर मिलता है तथा AE और BC बढ़ाने पर F पर मिलते हैं। CF की लंबाई ज्ञात कीजिए।
नीचे दी गयी आकृतियों में से कौन-सी आकृति निम्नलिखित गुणों को संतुष्ट करती है?
- सभी भुजाएँ बराबर हैं।
- सभी कोण समकोण हैं।
- सम्मुख भुजाएँ समांतर हैं।
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
सभी आयत समांतर चतुर्भुज होते हैं।
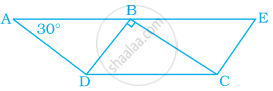
निम्न समांतर चतुर्भुज में, x और y के मान ज्ञात कीजिए –
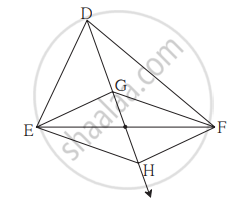
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।