Advertisements
Advertisements
Question
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।
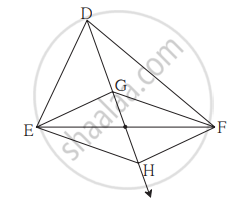
Solution
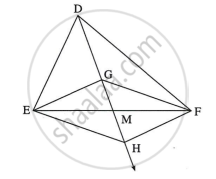
माना, बिंदु D से खींची गई माध्यिका भुजा EF को बिंदु M पर प्रतिच्छेदित करती है।
बिंदु G संगमन बिंदु है । ....(दत्त)
संगमन बिंदु, प्रत्येक माध्यिका को 2 : 1 के अनुपात में विभाजित करता है।
∴ DG : GM = 2 : 1
∴ `("DG")/("GM") = 2/1`
∴ DG = 2GH ....(i)
∴ DG = GM + MH ....(G-M-H)
∴ 2GM = GM +MH ....[(i) से]
∴ 2GM - GM = MH
∴ GM = MH ....(ii)
`square` GEHF में,
रेख GM ≅ रेख MH ....[(ii) से]
रेख EM ≅ रेख MF ....(बिंदु M, रेख EF का मध्यबिंदु है)
एक चतुर्भुज एक समांतर चतुर्भुज होता है, यदि इसके विकर्ण एक दूसरे को समद्विभाजित करते हैं।
`square` GEHF समांतर चतुर्भुज होता है।
APPEARS IN
RELATED QUESTIONS
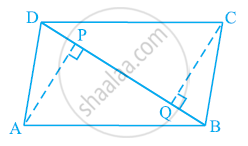
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:
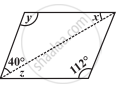
क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
निम्नलिखित के लिए कारण दीजिए:
वर्ग, आयत, समांतर चतुर्भुज और समचतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
एक समांतर चतुर्भुज के विकर्ण परस्पर लंब होते हैं। क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
समांतर चतुर्भुज ABCD के विकर्ण, AC पर बिंदु E और F इस प्रकार स्थित हैं कि AE = CF है। दर्शाइए कि BFDE एक समांतर चतुर्भुज है।
नीचे दी गयी आकृतियों में से कौन-सी आकृति निम्नलिखित गुणों को संतुष्ट करती है?
- सभी भुजाएँ बराबर हैं।
- सभी कोण समकोण हैं।
- सम्मुख भुजाएँ समांतर हैं।
सभी आयत समांतर चतुर्भुज होते हैं।
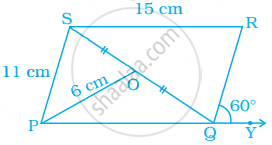
नीचे दिये समांतर चतुर्भुज PQRS में, O विकर्ण SQ का मध्य बिंदु है। ∠S, ∠R, PQ, QR और विकर्ण PR ज्ञात कीजिए।
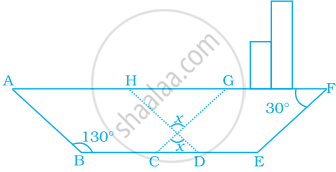
नीचे दिये गये एक जहाज कौँ आकृति में, ABDH और CEFG दो समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।