Advertisements
Advertisements
Question
सिद्ध कीजिए कि, आयत एक समांतर चतुर्भुज होता है।
Solution
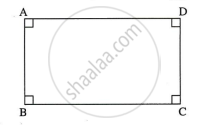
दत्त: `square` ABCD आयत है।
साध्य: `square` ABCD समांतर चतुर्भुज है।
उपपत्ति:
`square`ABCD आयत है।
∠A = ∠B = ∠C = ∠D = 90° ....(आयत के कोण)
∠A = ∠B = ∠C = ∠D .... (प्रत्येक कोण 90°)
एक चतुर्भुज एक समांतर चतुर्भुज होता है, यदि इसके सम्मुख कोणों के जोड़े सर्वांगसम हों।
∴ □ABCD एक समांतर चतुर्भुज है।
APPEARS IN
RELATED QUESTIONS
एक चतुर्भुज का नाम बताइए जिसके विकर्ण बराबर हों।
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
निम्न में से किस आकृति के लिए विकर्ण बराबर होते हैं?
यदि किसी चतुर्भुज के विकर्ण बराबर हों तथा परस्पर समद्विभाजित करें, तो वह होता है एक ______।
QR = 6 cm, PQ = 4 cm और ∠PQR = 90∘ के साथ एक समांतर चतुर्भुज की रचना की जाती है। तब PQRS है एक ______।
यदि एक समचतुर्भुज के विकर्ण बराबर हों, तो वह अवश्य ही आयत होगा।
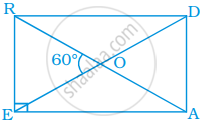
नीचे दिये आयत READ में, ∠EAR ,∠RAD और ∠ROD ज्ञात कीजिए।
एक आयत की रचना कीजिए, जिसकी एक भुजा 3 cm और विकर्ण 5 cm है।
आयत ABCD के विकर्ण परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AC = 8 सेमी तो BO = ? यदि ∠CAD = 35° तो ∠ACB = ?
नीचे दिए गए कथन सत्य हैं या असत्य, कारण सहित लिखिए।
प्रत्येक समांतर चतुर्भुज, आयत होता है।
