Advertisements
Advertisements
Question
यदि एक समचतुर्भुज के विकर्ण बराबर हों, तो वह अवश्य ही आयत होगा।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण:
हम जानते हैं कि आयतों के विकर्ण बराबर होते हैं।
तो, यह निश्चित रूप से एक आयत है।
APPEARS IN
RELATED QUESTIONS
उन सभी चतुर्भुजों की पहचान कीजिए जिनमें चार समकोण हो।
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
एक सम अष्टभुज (regular octagon) का एक रफ़ चित्र खींचिए। [यदि आप चाहें, तो वर्गांकित कागज़ (squared paper) का प्रयोग कर सकते हैं।] इस अष्टभुज के चार शीर्षों को जोड़कर एक आयत खींचिए।
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
QR = 6 cm, PQ = 4 cm और ∠PQR = 90∘ के साथ एक समांतर चतुर्भुज की रचना की जाती है। तब PQRS है एक ______।
आयत एक सम चतुर्भुज है।
प्रत्येक आयत एक समलंब है।
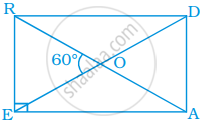
नीचे दिये आयत READ में, ∠EAR ,∠RAD और ∠ROD ज्ञात कीजिए।
चतुर्भुज EFGH एक आयत है, जिसमें J दोनों विकर्णों का प्रतिच्छेद बिंदु है। x का मान ज्ञात कीजिए, JF = 8x + 4 और EG = 24x − 8 है।
आयत ABCD के विकर्ण परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AC = 8 सेमी तो BO = ? यदि ∠CAD = 35° तो ∠ACB = ?
