Advertisements
Advertisements
Question
चतुर्भुज EFGH एक आयत है, जिसमें J दोनों विकर्णों का प्रतिच्छेद बिंदु है। x का मान ज्ञात कीजिए, JF = 8x + 4 और EG = 24x − 8 है।
Solution
दिया गया है, EFGH एक आयत है जिसके विकर्ण बिंदु J पर प्रतिच्छेद करते हैं।
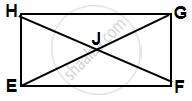
हम जानते हैं कि, आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं।
तब, EG = 2 × JF
⇒ 24x – 8 = 2(8x + 4)
⇒ 24x – 8 = 16x + 8
⇒ 24x – 16x = 8 + 8
⇒ 8x = 16
⇒ x = 2
APPEARS IN
RELATED QUESTIONS
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग को एक विशेष प्रकार का आयत समझा जा सकता है।
निम्न में से किस के लिए, सभी कोण बराबर होते हैं?
निम्न में से किस आकृति के लिए विकर्ण बराबर होते हैं?
QR = 6 cm, PQ = 4 cm और ∠PQR = 90∘ के साथ एक समांतर चतुर्भुज की रचना की जाती है। तब PQRS है एक ______।
सभी वर्ग आयत होते हैं।
यदि एक समचतुर्भुज के विकर्ण बराबर हों, तो वह अवश्य ही आयत होगा।
एक आयत ABCD में, AB = 25 cm और BC = 15 है। ∠C का समद्विभाजिक AB को किस अनुपात में विभाजित करता है?
एक आयत की रचना कीजिए, जिसकी एक भुजा 3 cm और विकर्ण 5 cm है।
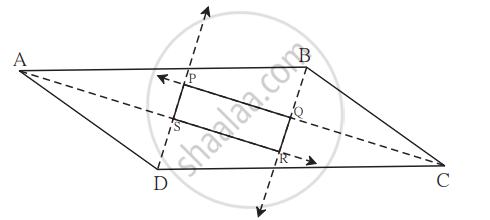
सिद्ध कीजिए कि, समांतर चतुर्भुज के चारों कोणों के समद्विभाजकों से बना चतुर्भुज आयत होता है।