Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि, आयत एक समांतर चतुर्भुज होता है।
उत्तर
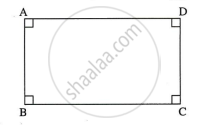
दत्त: `square` ABCD आयत है।
साध्य: `square` ABCD समांतर चतुर्भुज है।
उपपत्ति:
`square`ABCD आयत है।
∠A = ∠B = ∠C = ∠D = 90° ....(आयत के कोण)
∠A = ∠B = ∠C = ∠D .... (प्रत्येक कोण 90°)
एक चतुर्भुज एक समांतर चतुर्भुज होता है, यदि इसके सम्मुख कोणों के जोड़े सर्वांगसम हों।
∴ □ABCD एक समांतर चतुर्भुज है।
APPEARS IN
संबंधित प्रश्न
बताइए कैसे एक वर्ग एक आयत है।
यदि किसी समांतर चतुर्भुज के आसन्न कोण बराबर हों, तो वह है एक –
सभी वर्ग आयत होते हैं।
प्रत्येक समांतर चतुर्भुज एक आयत है।
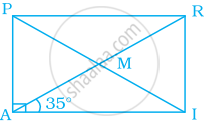
नीचे दिये आयत PAIR में, ∠ARI, ∠RMI और ∠PMA ज्ञात कीजिए।
एक आयत की रचना कीजिए, जिसकी एक भुजा 3 cm और विकर्ण 5 cm है।
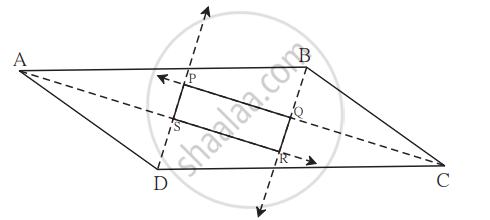
सिद्ध कीजिए कि, समांतर चतुर्भुज के चारों कोणों के समद्विभाजकों से बना चतुर्भुज आयत होता है।
आयत ABCD के विकर्ण परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AC = 8 सेमी तो BO = ? यदि ∠CAD = 35° तो ∠ACB = ?
नीचे दिए गए कथन सत्य हैं या असत्य, कारण सहित लिखिए।
प्रत्येक आयत समांतर चतुर्भुज होता है।
किसी आयत की संलग्न भुजाएँ क्रमशः 7 सेमी तथा 24 सेमी हैं तो उस चतुर्भुज की विकर्ण की लंबाई ज्ञात कीजिए।
