Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि, समांतर चतुर्भुज के चारों कोणों के समद्विभाजकों से बना चतुर्भुज आयत होता है।
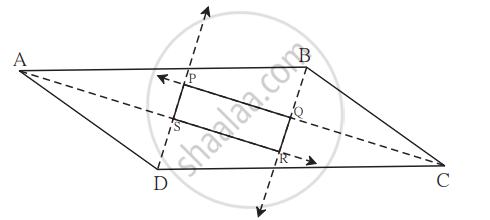
उत्तर
दत्त: `square` ABCD समांतर चतुर्भुज है।
साध्य: `square` PQRS आयत है।
उपपत्ति:
`square` ABCD समांतर चतुर्भुज है। ...(दत्त)
∠ADC + ∠BCD = 180° ...(समांतर चतुर्भुज के क्रमिक कोण संपूरक होते हैं।)
प्रत्येक पक्ष में `1/2`, से गुणा करने पर,
`1/2` ∠ADC + `1/2` ∠BCD = `1/2xx180°` ...(i)
परंतु, `1/2` ∠ADC = ∠PDC ...(किरण DP, ∠ADC को समद्विभाजित करती है) ...(ii)
तथा `1/2` ∠BCD = ∠PCD ...(किरण CP, ∠BCD को समद्विभाजित करती है) ...(iii)
∴ ∠PDC + ∠PCD = 90° ...[(i), (ii) और (iii) से] ...(iv)
ΔPDC में,
∠PDC + ∠PCD + ∠DPC = 180° ...(त्रिभुज के तीनो कोणों के मापों का योगफल 180° होता है।)
∴ 90° + ∠DPC = 180° ...[(iv) से]
∴ ∠DPC = 180° - 90°
∴ ∠DPC = 90°
अर्थात ∠SPQ = 90° ...(D-S-P, P-Q-C) ...(v)
इसी प्रकार, हम सिद्ध कर सकते हैं कि, ∠SRQ = 90° ...(vi)
इसी प्रकार, ∠ASD = 90° तथा ∠BQC = 90° ...(vii)
∠PSR = ∠ASD ...(शीर्षाभिमुख कोण)
∴ ∠PSR = 90° ...[(vii) से] ...(viii)
इसी प्रकार, ∠PQR = 90° ...(ix)
`square` PQRS में,
∠SPQ = ∠SRQ = ∠PSR = ∠PQR = 90° ...[(v), (vi), (viii) और (ix) से]
∴ `square` PQRS आयत है।
APPEARS IN
संबंधित प्रश्न
एक चतुर्भुज का नाम बताइए जिसके विकर्ण बराबर हों।
निम्न में से किस आकृति के लिए विकर्ण बराबर होते हैं?
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
यदि किसी चतुर्भुज के विकर्ण बराबर हों तथा परस्पर समद्विभाजित करें, तो वह होता है एक ______।
QR = 6 cm, PQ = 4 cm और ∠PQR = 90∘ के साथ एक समांतर चतुर्भुज की रचना की जाती है। तब PQRS है एक ______।
प्रत्येक आयत एक समलंब है।
रेखा l रेखा m के समांतर है तथा एक तिर्यक रेखा p क्रमशः इन्हें X और Y पर प्रतिच्छेद करती है। X और Y पर स्थित अंतःकोणों के समद्विभाजक P और Q प्रतिच्छेद करते हैं। क्या PXQY एक आयत है? कारण दीजिए।
एक आयत की रचना कीजिए, जिसकी एक भुजा 3 cm और विकर्ण 5 cm है।
सिद्ध कीजिए कि, आयत एक समांतर चतुर्भुज होता है।
आयत PQRS के विकर्ण परस्पर बिंदु M पर प्रतिच्छेदित करते हैं। यदि `angle`QMR = 50° तो `angle`MPS का माप ज्ञात कीजिए।
