Advertisements
Advertisements
प्रश्न
संलग्न आकृति में समांतर चतुर्भुज `square` ABCD की भुजाओं पर P, Q, R, S इस प्रकार है कि, AP = BQ = CR = DS तो सिद्ध कीजिए कि `square` PQRS समांतर चतुर्भुज है।

उत्तर
दत्त: `square` ABCD समांतर चतुर्भुज है।
AP = BQ = CR = DS
साध्य: `square` PQRS समांतर चतुर्भुज है।
उपपत्ति:
AP = CR .....(दत्त) ...(i)
`square` ABCD समांतर चतुर्भुज है।
AB = CD ...( समांतर चतुर्भुज की सम्मुख भुजाएँ)
∴ AP + PB = CR + RD ....[A-P-B, D-R-C] ....(ii)
∴ PB = RD .....[(i) और (ii) से] ...(iii)
∠ABC ≅ ∠ADC ....(समांतर चतुर्भुज के सम्मुख कोण)
अर्थात, ∠PBQ ≅ ∠RDS ...(A-P-B, B-Q-C, C-R-D और A-S-D) ....(iv)
ΔPBQ तथा ΔRDS में,
रेख PB ≅ रेख RD ....[(iii) से]
∠PBQ ≅ ∠RDS ....[(iv) से]
रेख BQ ≅ रेख SD ....(दत्त)
∴ ΔPBQ ≅ ΔRDS ....(सर्वांगसमता की भु-को-भु कसौटी)
रेख PQ ≅ रेख RS ....(स.त्रि.सं.भु) .....(v)
इस प्रकार, हम सिद्ध कर सकते हैं कि, ΔPAS ≅ ΔRCQ,
∴ रेख PS ≅ रेख RQ ....(vi)
`square` PQRS में,
रेख PQ ≅ रेख RS ....[(v) से]
रेख PS ≅ रेख RQ ....[(vi) से]
यदि किसी चतुर्भुज की सम्मुख भुजाएँ सर्वांगसम हो, तो वह समांतर चतुर्भुज होता है।
∴ `square` PQRS समांतर चतुर्भुज है।
APPEARS IN
संबंधित प्रश्न
एक समांतर चतुर्भुज के विकर्ण परस्पर लंब होते हैं। क्या यह कथन सत्य है? अपने उत्तर के लिए कारण दीजिए।
एक चतुर्भुज ABCD के विकर्ण परस्पर समद्विभाजित करते हैं। यदि ∠A = 35° है, तो ∠B निर्धारित कीजिए।
ABCD एक समलंब है जिसमें AB || DC और ∠A = ∠B = 45° है। इस समलंब के कोण C और D ज्ञात कीजिए।
एक समांतर चतुर्भुज के एक अधिक कोण के शीर्ष से खींचे गए उस समांतर चतुर्भुज के दो शीर्षलंबों के बीच का कोण 60° है। इस समांतर चतुर्भुज के सभी कोण ज्ञात कीजिए।
नीचे दी गयी आकृति में, ABCD और BDCE एक ही आधार DC पर दो समांतर चतुर्भुज हैं। यदि BC ⊥ BD है, तो ∠BEC बराबर है –
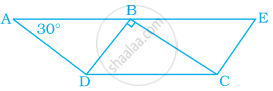
किसी चतुर्भुज के विकर्णों का प्रतिच्छेद बिंदु इनमें से एक को 1: 2 के अनुपात में विभाजित करता है। क्या यह एक समांतर चतुर्भुज होगा? क्यों और क्यों नहीं?
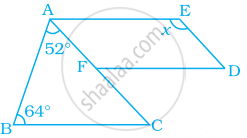
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
एक समांतर चतुर्भुज ABCD की रचना कीजिए, जिसमें AB = 4cm, BC = 5 cm और ∠B = 60∘ है।
एक समांतर चतुर्भुज HOME की रचना कीजिए, जिसमें HO = 6 cm, HE = 4 cm और OE = 3 cm है।
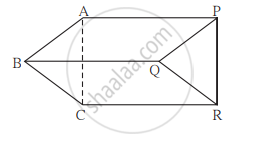
संलग्न आकृति में रेख AB || रेख PQ , रेख AB ≅ रेख PQ, रेख AC || रेख PR, रेख AC ≅ रेख PR तो सिद्ध कीजिए कि रेख BC || रेख QR तथा रेख BC ≅ रेख QR