Advertisements
Advertisements
प्रश्न
आयत PQRS के विकर्ण परस्पर बिंदु M पर प्रतिच्छेदित करते हैं। यदि `angle`QMR = 50° तो `angle`MPS का माप ज्ञात कीजिए।
उत्तर
आकृति:
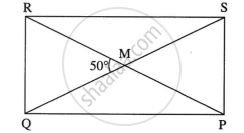
हल:
`square` PQRS एक आयत है।
∴ PM = `1/2` PR …(i)
MS = `1/2` QS …(ii) ...(आयत के विकर्ण एक दूसरे को समद्विभाजित करते हैं।)
साथ ही, PR = QS ....(iii) ...(आयत के विकर्ण सर्वांगसम होते हैं।)
∴ PM = MS ...[(i), (ii) और (iii) से] ...(iv)
∆PMS में,
PM = MS ...[(iv) से]
∴ ∠MSP = ∠MPS = x° …(v) ...(समद्विबाहु त्रिभुज के प्रमेय से)
∠PMS = ∠QMR = 50° …(vi) ...(शीर्षाभिमुख कोण)
∆MPS में,
∠PMS + ∠MPS + ∠MSP = 180° ...(त्रिभुज के तीनों कोणों की मापों का योग 180° होता है।)
∴ 50° + x + x = 180° ...[(v) और (vi) से]
∴ 50° + 2x = 180
∴ 2x = 180 - 50
∴ 2x = 130
∴ x = `130/2` = 65°
∴ ∠MPS = 65° ...[(v) से]
APPEARS IN
संबंधित प्रश्न
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
यदि किसी समांतर चतुर्भुज के आसन्न कोण बराबर हों, तो वह है एक –
आयत एक सम चतुर्भुज है।
प्रत्येक आयत एक समलंब है।
एक आयत ABCD में, AB = 25 cm और BC = 15 है। ∠C का समद्विभाजिक AB को किस अनुपात में विभाजित करता है?
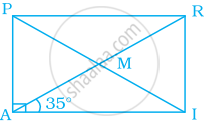
नीचे दिये आयत PAIR में, ∠ARI, ∠RMI और ∠PMA ज्ञात कीजिए।
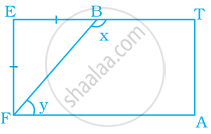
एक खेल का मैदान एक आयत ATEF के रूप का है। दो खिलाड़ी बिंदु F और B पर खड़ हैं, जहाँ EF = EB है। x और y के मान ज्ञात कीजिए।
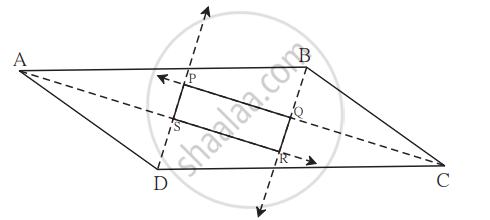
रेखा l रेखा m के समांतर है तथा एक तिर्यक रेखा p क्रमशः इन्हें X और Y पर प्रतिच्छेद करती है। X और Y पर स्थित अंतःकोणों के समद्विभाजक P और Q प्रतिच्छेद करते हैं। क्या PXQY एक आयत है? कारण दीजिए।
सिद्ध कीजिए कि, आयत एक समांतर चतुर्भुज होता है।
सिद्ध कीजिए कि, समांतर चतुर्भुज के चारों कोणों के समद्विभाजकों से बना चतुर्भुज आयत होता है।