Advertisements
Advertisements
प्रश्न
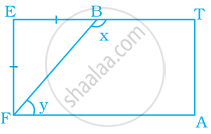
एक खेल का मैदान एक आयत ATEF के रूप का है। दो खिलाड़ी बिंदु F और B पर खड़ हैं, जहाँ EF = EB है। x और y के मान ज्ञात कीजिए।
उत्तर
दिया गया है, एक आयत ATEF जिसमें EF = EB है।
तब, ΔFEB एक समद्विबाहु त्रिभुज है।
इसलिए, त्रिभुज के कोणों के योग गुण के अनुसार, हमें प्राप्त होता है।
∠EFB + ∠EBF + ∠FEB = 180° ...[त्रिभुज के कोणों के योग का गुण]
⇒ ∠EFB + ∠EBF + 90° = 180° ...[∵ आयत में प्रत्येक कोण 90° का होता है।]
⇒ 2∠EFB = 90° ...[∵ ∠EFB = ∠EBF]
∠EFB = 45° और ∠EBF = 45°
अब, ∠x = 180° – 45° = 135° ...[रैखिक युग्म]
और ∠EFB + ∠y = 90° ...[∵ एक आयत में, प्रत्येक कोण 90° का होता है।]
⇒ ∠y = 90° – 45° = 45°
APPEARS IN
संबंधित प्रश्न
बताइए कैसे एक वर्ग एक आयत है।
निम्न में से किस आकृति के लिए विकर्ण बराबर होते हैं?
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
सभी वर्ग आयत होते हैं।
प्रत्येक आयत एक समलंब है।
एक आयत ABCD में, AB = 25 cm और BC = 15 है। ∠C का समद्विभाजिक AB को किस अनुपात में विभाजित करता है?
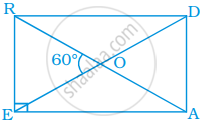
नीचे दिये आयत READ में, ∠EAR ,∠RAD और ∠ROD ज्ञात कीजिए।
रेखा l रेखा m के समांतर है तथा एक तिर्यक रेखा p क्रमशः इन्हें X और Y पर प्रतिच्छेद करती है। X और Y पर स्थित अंतःकोणों के समद्विभाजक P और Q प्रतिच्छेद करते हैं। क्या PXQY एक आयत है? कारण दीजिए।
आयत ABCD के विकर्ण परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AC = 8 सेमी तो BO = ? यदि ∠CAD = 35° तो ∠ACB = ?
नीचे दिए गए कथन सत्य हैं या असत्य, कारण सहित लिखिए।
प्रत्येक समांतर चतुर्भुज, आयत होता है।
