Advertisements
Advertisements
Question
एक खेल का मैदान एक आयत ATEF के रूप का है। दो खिलाड़ी बिंदु F और B पर खड़ हैं, जहाँ EF = EB है। x और y के मान ज्ञात कीजिए।
Advertisements
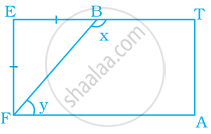
Solution
दिया गया है, एक आयत ATEF जिसमें EF = EB है।
तब, ΔFEB एक समद्विबाहु त्रिभुज है।
इसलिए, त्रिभुज के कोणों के योग गुण के अनुसार, हमें प्राप्त होता है।
∠EFB + ∠EBF + ∠FEB = 180° ...[त्रिभुज के कोणों के योग का गुण]
⇒ ∠EFB + ∠EBF + 90° = 180° ...[∵ आयत में प्रत्येक कोण 90° का होता है।]
⇒ 2∠EFB = 90° ...[∵ ∠EFB = ∠EBF]
∠EFB = 45° और ∠EBF = 45°
अब, ∠x = 180° – 45° = 135° ...[रैखिक युग्म]
और ∠EFB + ∠y = 90° ...[∵ एक आयत में, प्रत्येक कोण 90° का होता है।]
⇒ ∠y = 90° – 45° = 45°
APPEARS IN
RELATED QUESTIONS
एक चतुर्भुज का नाम बताइए जिसके विकर्ण बराबर हों।
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
QR = 6 cm, PQ = 4 cm और ∠PQR = 90∘ के साथ एक समांतर चतुर्भुज की रचना की जाती है। तब PQRS है एक ______।
प्रत्येक समांतर चतुर्भुज एक आयत है।
PQRS एक आयत है। S से PR पर डाला गया लंब ST कोण S को 2:3 के अनुपात में विभाजित करता है। ∠TPQ को ज्ञात कीजिए।
चतुर्भुज EFGH एक आयत है, जिसमें J दोनों विकर्णों का प्रतिच्छेद बिंदु है। x का मान ज्ञात कीजिए, JF = 8x + 4 और EG = 24x − 8 है।
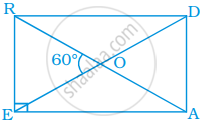
सिद्ध कीजिए कि, आयत एक समांतर चतुर्भुज होता है।
सिद्ध कीजिए कि, समांतर चतुर्भुज के चारों कोणों के समद्विभाजकों से बना चतुर्भुज आयत होता है।
आयत ABCD के विकर्ण परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AC = 8 सेमी तो BO = ? यदि ∠CAD = 35° तो ∠ACB = ?
