Advertisements
Advertisements
प्रश्न
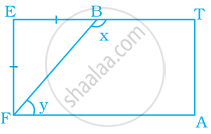
एक खेल का मैदान एक आयत ATEF के रूप का है। दो खिलाड़ी बिंदु F और B पर खड़ हैं, जहाँ EF = EB है। x और y के मान ज्ञात कीजिए।
उत्तर
दिया गया है, एक आयत ATEF जिसमें EF = EB है।
तब, ΔFEB एक समद्विबाहु त्रिभुज है।
इसलिए, त्रिभुज के कोणों के योग गुण के अनुसार, हमें प्राप्त होता है।
∠EFB + ∠EBF + ∠FEB = 180° ...[त्रिभुज के कोणों के योग का गुण]
⇒ ∠EFB + ∠EBF + 90° = 180° ...[∵ आयत में प्रत्येक कोण 90° का होता है।]
⇒ 2∠EFB = 90° ...[∵ ∠EFB = ∠EBF]
∠EFB = 45° और ∠EBF = 45°
अब, ∠x = 180° – 45° = 135° ...[रैखिक युग्म]
और ∠EFB + ∠y = 90° ...[∵ एक आयत में, प्रत्येक कोण 90° का होता है।]
⇒ ∠y = 90° – 45° = 45°
APPEARS IN
संबंधित प्रश्न
एक चतुर्भुज का नाम बताइए जिसके विकर्ण बराबर हों।
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
सभी वर्ग आयत होते हैं।
आयत एक सम चतुर्भुज है।
यदि एक समचतुर्भुज के विकर्ण बराबर हों, तो वह अवश्य ही आयत होगा।
प्रत्येक आयत एक समलंब है।
एक आयत की रचना कीजिए, जिसकी एक भुजा 3 cm और विकर्ण 5 cm है।
सिद्ध कीजिए कि, आयत एक समांतर चतुर्भुज होता है।
नीचे दिए गए कथन सत्य हैं या असत्य, कारण सहित लिखिए।
प्रत्येक समांतर चतुर्भुज, आयत होता है।
किसी आयत की संलग्न भुजाएँ क्रमशः 7 सेमी तथा 24 सेमी हैं तो उस चतुर्भुज की विकर्ण की लंबाई ज्ञात कीजिए।
