Advertisements
Advertisements
प्रश्न
एक समांतर चतुर्भुज MODE में, ∠M कोण ∠O के समद्विभाजक Q पर मिलते हैं। ∠MQO की माप ज्ञात कीजिए।
उत्तर
मान लीजिए कि MODE एक समांतर चतुर्भुज है और Q, ∠M और ∠O के समद्विभाजक का प्रतिच्छेद बिंदु है।
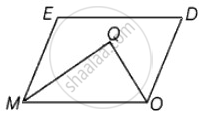
चूँकि, MODE एक समांतर चतुर्भुज है।
∴ ∠EMO + ∠DOM = 180° ...[∵ आसन्न कोण पूरक हैं।]
⇒ `1/2` ∠EMO + `1/2` ∠DOM = 90° ...[दोनों पक्षों को 2 से विभाजित करने पर]
⇒ ∠QMO + ∠QOM = 90° ...(i)
अब, ΔMOQ में,
∠QOM + ∠QMO + ∠MQO = 180° ...[त्रिभुज के कोणों के योग का गुण]
⇒ 90° + ∠MQO = 180° ...[समीकरण (i) से]
∴ ∠MQO = 180° – 90° = 90°
APPEARS IN
संबंधित प्रश्न
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि:
- ABCD एक वर्ग है।
- विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
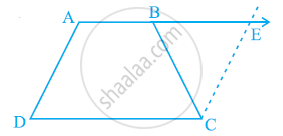
ABCD एक समलंब है, जिसमें AB || DC और AD = BC है (देखिए आकृति में)। दर्शाइए कि
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- विकर्ण AC = विकर्ण BD है।
[संकेत: AB को बढ़ाइए और C से होकर DA के समांतर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
निम्न समांतर चतुर्भुज में अज्ञात x,y,z के मानों को ज्ञात कीजिए:

निम्न समांतर चतुर्भुज में अज्ञात x, y, z के मानों को ज्ञात कीजिए:

क्या एक चतुर्भुज ABCD समांतर चतुर्भुज हो सकता है यदि ∠D +∠B = 180°?
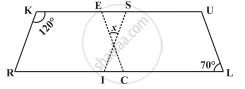
दी गई आकृति में RISK तथा CLUE दोनों समांतर चतुर्भुज हैं, x का मान ज्ञात कीजिए।
बताइए कैसे एक वर्ग एक समांतर चतुर्भुज है।
निम्नलिखित आकृति में, यह दिया है कि BDEF और FDCE समांतर चतुर्भुज हैं। क्या आप कह सकते हैं कि BD = CD है? क्यों और क्यों नहीं?

एक समांतर चतुर्भुज के एक अधिक कोण के शीर्ष से खींचे गए उस समांतर चतुर्भुज के दो शीर्षलंबों के बीच का कोण 60° है। इस समांतर चतुर्भुज के सभी कोण ज्ञात कीजिए।
ABCD एक समचतुर्भुज है, जिसमें D से AB पर शीर्षलंब AB को समद्विभाजित करता है। समचतुर्भुज के कोण ज्ञात कीजिए।
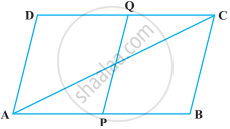
एक समांतर चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD पर क्रमश : बिंदु P और Q इस प्रकार लिए गए हैं कि AP = CQ है। (आकृति)। दर्शाइए कि AC और PQ परस्पर समद्विभाजित करते हैं।
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
किसी चतुर्भुज के विकर्णों का प्रतिच्छेद बिंदु इनमें से एक को 1: 2 के अनुपात में विभाजित करता है। क्या यह एक समांतर चतुर्भुज होगा? क्यों और क्यों नहीं?
ABCD एक समांतर चतुर्भुज है। कोण A का समद्विभाजक CD को X पर प्रतिच्छेद करता है तथा कोण C का समद्विभाजक AB को Y पर प्रतिच्छेद करता है। क्या AXCY एक समांतर चतुर्भुज है? कारण दीजिए।
समांतर ABCD में, ∠A का समद्विभाजक BC को समद्विभाजित करता है। क्या कोण B का समद्विभाजक AD को भी समद्विभाजित करता है? कारण दीजिए।
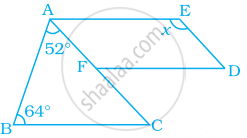
निम्न आकृति में, FD || BC || AE है और AC || ED है। x का मान ज्ञात कीजिए –
आकृति में `square` ABCD समांतर चतुर्भुज है। किरण AB पर बिंदु E इस प्रकार है कि BE = AB तो सिद्ध कीजिए कि रेखा ED यह रेख BC को बिंदु F पर समद्विभाजित करती है।

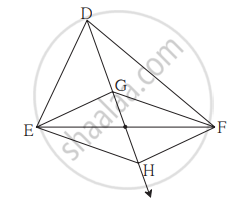
आकृति में, बिंदु G, ΔDEF की माध्यिकाओं का संगामी बिंदु है। किरण DG पर बिंदु H इस प्रकार लें कि D-G-H तथा DG = GH, हो तो सिद्ध कीजिए कि `square` GEHF समांतर चतुर्भुज है।